numpy.log1p() in Python: For Natural Logarithmic Calculations

And we are back again with a new function to add to our logarithmic series. This time we will explore the log1p() function, which will return the natural log of the given value. We will see what the natural log is, why it is important to calculate, and how we can calculate it, every answer will be provided. All you need to do is follow along with us, so let’s begin.

What Is a Natural Logarithm Function?

The ln (natural logarithm function) tells us how much we need to multiply “e” to get a certain number. For example, if ln(x) = 2, it means we need to multiply “e” by itself twice to get x. “e” is a special number like 2 or 3, but it’s about 2.71828. It’s useful in many areas of math because it pops up naturally in lots of situations.

Key Points:

ln(1) = 0: This means if we multiply “e” by itself zero times (which means not multiplying at all), we get 1.
ln(e) = 1: Here, we see that if we multiply “e” by itself once, we get “e” itself.
You can’t do ln of a negative number or zero.

When we plot ln on a graph, it starts at 0 when x is 1 and goes up slowly at first, then faster as x gets bigger.

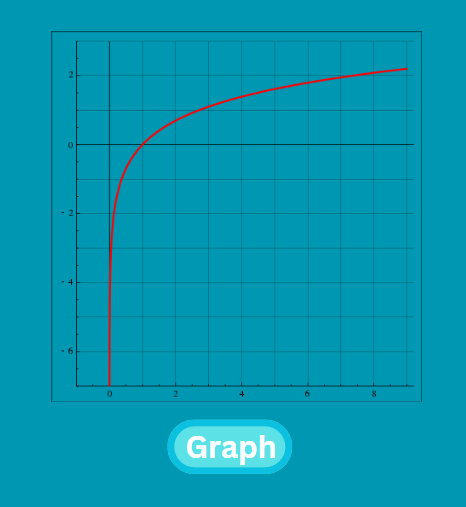
Now, the function we want to talk about in this tutorial is ln⁡(x+1), it is the natural logarithm of x+1. It’s used to simplify data, study growth patterns, and solve equations in math and statistics. It’s related to the natural logarithm because it’s just ln⁡(y) where y=x+1.

Wondering how we can compute this in Python? Here comes numpy.log1p.

Introducing numpy.log1p

numpy.log1p(x) helps find the natural logarithm of a number plus one. It’s better for small numbers because it keeps the precision, unlike adding 1 first and then finding the logarithm.

Syntax:

The syntax of the given function looks like this:

numpy.log1p(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj])

Let’s discuss each parameter:

x: This is the number or list of numbers you want to calculate the natural logarithm of.
out: You can specify where you want the result to be placed.
where: This lets you set conditions for which elements you want to calculate in the output. By default, it calculates all elements.
dtype: This is the type of data you want the result to be. If you don’t specify, it figures it out from the input.
Other parameters, like casting and order, are about how the arrays are handled in memory and type conversions, but you usually don’t need to worry about them unless you’re doing something really specific.

Key Features:

Precision: log1p() keeps accuracy for tiny values, unlike log(x + 1).
Avoids Issues: It sidesteps problems with underflow for small x.
Inverse: It pairs with expm1(), handling small values accurately.
Broadcasting: Works with arrays of different sizes.
Efficiency: Designed for speed, especially with large array

Using numpy.log1p in Python

Now that we’ve gone through the theory part, let’s jump into some real examples so we can get a clearer understanding of how to use this function in Python.

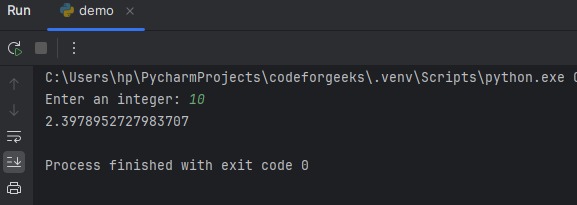
Example 1: First, we will look at the basic usage.

import numpy as np

num = int(input("Enter an integer: "))
result = np.log1p(num)
print(result)

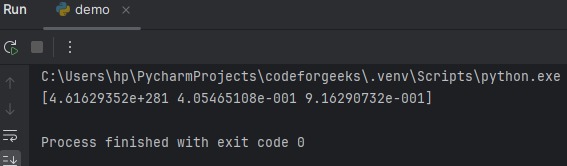
Example 2: We can apply conditions to the calculation.

import numpy as np

x = np.array([-0.5, 0.5, 1.5])
result = np.log1p(x, where=x>=0) 
print(result)

Here we use the ‘where‘ parameter to compute only for non-negative elements. It may generate garbage value for false conditions.

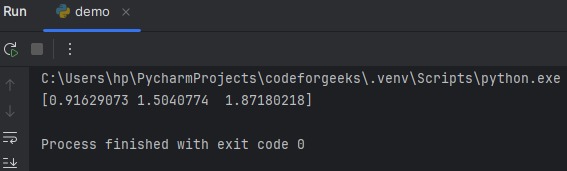
Example 3: The function supports broadcasting and allows operations on arrays of different shapes and sizes.

import numpy as np

x = np.array([0.5, 1.5, 2.5])
y = np.array([1, 2, 3])
result = np.log1p(x + y) 
print(result)

Here, the function adds two arrays element-wise before taking the logarithm.

Example 4: This function can handle underflow and overflow conditions without losing precision. Let’s see how.

import numpy as np

x = np.array([1e-200, 1e-300, 1e-400])
result = np.log1p(x)
print(result)

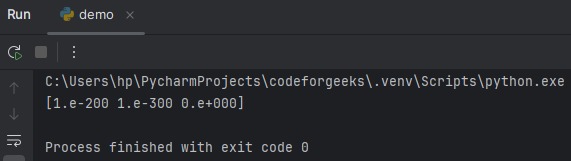
Overflow happens when a number gets too big for the computer to handle, while underflow occurs when a number becomes too small to be accurately represented. So, in the example provided, numpy.log1p() is used to calculate the natural logarithm of these extremely small numbers. What’s impressive is that it does this without causing underflow issues.

Conclusion

And we’ve reached the bottom line. I hope that you now have a strong understanding of the log1p function and how it works. We’ve learned about new terms like underflow and overflow conditions and how nicely NumPy handles them. We have more in the NumPy logarithm series, such as NumPy log2 and NumPy log10, so be sure to check them out!