Understanding numpy.hypot() in Python

Have you ever needed to find the distance between two points in space? In this guide, we will solve this problem using the NumPy hypot() function. By using hypot, we can accurately measure the straight-line distance between two points in space, typically known as the hypotenuse. Let us look at this function in detail.

What is Euclidean Distance?

Euclidean Distance measures a straight-line distance between two points in space.

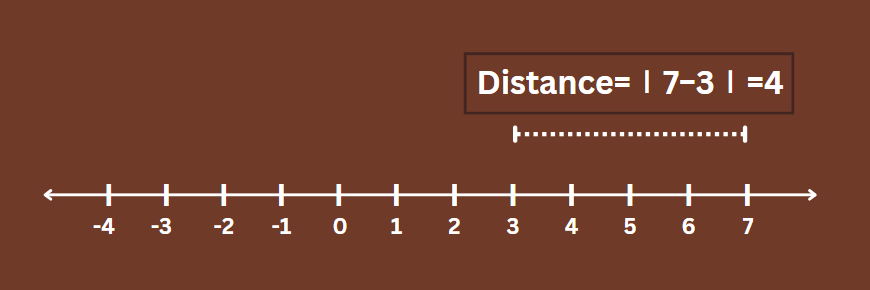
Let me illustrate this with an example. Consider a number line (a one-dimensional spatial). If you have two points such as 3 and 7, it simply means that their Euclidean Distance is the absolute difference between those two points.

Now consider a flat map or plane that represents a two-dimensional space. You want to determine the distance covered by moving from position (1,2) to position (4,6). To find the Euclidean Distance, use the Pythagorean theorem:

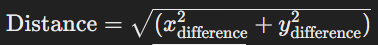
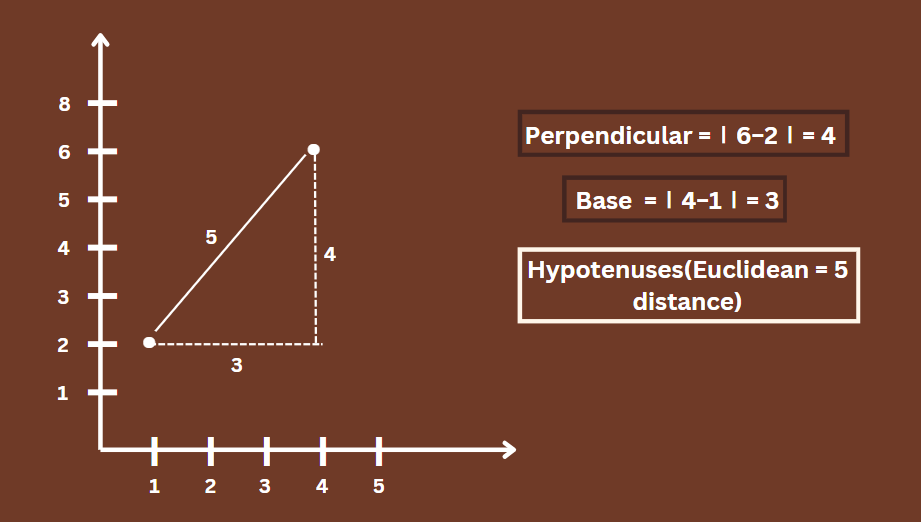
Now that we are speaking of the Pythagorean theorem, let’s first talk about hypotenuse. When we draw a right-angled triangle, the side just opposite the right angle is what we call hypotenuse, and it is also the longest side of that triangle. In a 2D plane, the Euclidean distance between two points (1, 2) and (4, 6) is the length of the hypotenuse of a right triangle formed by these points.

Introducing numpy.hypot() Function

The numpy.hypot function in the NumPy library calculates the Euclidean distance between two points in a 2D space. It finds the length of the hypotenuse of a right-angled triangle when given the lengths of the other two sides. This function is useful for measuring distances in machine learning, computer vision, and physics.

Syntax:

Let’s look at the format of this function.

numpy.hypot(x1, x2, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True, **kwargs)

Here is what each parameter means.

x1, x2: These are the input values, representing the lengths of the two sides of a right-angled triangle.
out (optional): An optional array to store the result. It should have the same shape as the expected output.
where (optional): A condition that determines where the result should be computed. If True, the result is stored in out, otherwise, out keeps its original value.
casting (optional): It determines how data types are cast.
order (optional): Specified memory layout of resulting array. Choices include ‘C’ (row-major), ‘F’ (column-major), ‘A‘ (any) or ‘K’(keep input order).
dtype (optional): Result’s desired data type.
subok (optional): If True, allows sub-classes to be passed through, otherwise, converts to the base class array.
kwargs: This provides additional optional arguments for this function.

Working:

Suppose we have two inputs, x1(Base) and x2(Perpendicular), representing the lengths of the two sides of a right-angled triangle. The numpy.hypot calculates the hypotenuse — the longest side, using this formula:

This hypotenuse represents the Euclidean distance from the origin to the point (x1,x2) in a two-dimensional cartesian plane.

Well, this function directly computes these powers and square roots for you. But if you only need to compute the powers at any time, you can see how NumPy’s power function helps us with that.

Examples of numpy.hypot in Python

Now, let’s implement the theory we just learned into code.

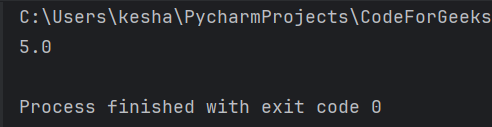
Example 1: Let’s see the simplest case, calculating the hypotenuse for a triangle with sides 3 and 4.

import numpy as np

x1 = 3
x2 = 4

distance = np.hypot(x1, x2)
print(distance)

Output:

Example 2: Now we will demonstrate how it can handle array inputs, calculating the hypotenuses for multiple pairs of sides.

import numpy as np

x1 = np.array([3, 5, 8])
x2 = np.array([4, 12, 15])

distances = np.hypot(x1, x2)
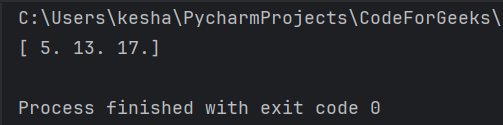
print(distances)

Now, in this case, the function would calculate the hypotenuse element-wise and then form a result array. For example, for 3 and 4, it’s 5, for 5 and 12, it’s 13, and so on. Therefore, the result would contain 5, 13, 17.

Output:

Example 3: Let’s utilize broadcasting, where a single value for x2 is applied to each element in the array x1.

import numpy as np

x1 = np.array([3, 5, 8])
x2 = 4

distances = np.hypot(x1, x2)
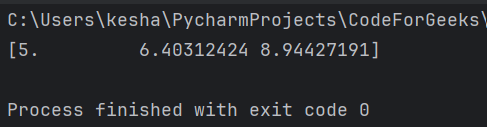
print(distances)

This code calculates the distance between each element in array x1 and the scalar value x2. It computes the hypotenuse element-wise, considering each element of x1 as one side and x2 as the other side, and then prints the resulting distances.

Output:

Conclusion

This one was easy and fun, right? Here, we started by understanding what Euclidean distance is and how it relates to the hypotenuse. We also learned about the NumPy tool for finding the hypotenuse which is hypot, went through its syntax and workings, and gained clarity through practical examples. Feel free to experiment with this concept in your projects.

Wondering what to read next? Well, let me help you with that decision. Wouldn’t it be nice to know how NumPy helps us to calculate gradients of array inputs in Python?