How to Perform Einstein Summation in Python Using numpy.einsum()

In Python, the concept of Einstein summation helps us simplify the calculations of arrays. It provides a great help in solving matrices, particularly calculating their cross-product, dot product, sum of diagonals, etc. In this article, let us explore this concept and understand the numpy.einsum() function.

Understanding Einstein Summation

Einstein summation is something that helps us to work with arrays and tensors. It helps us to simplify expressions such as matrices, tensors and summation of vectors.

There are three vital rules about this convection to keep in mind:

When an index is repeated, it is summed over automatically, without any need to write the summation symbol.
Each index can only repeat itself twice in any term.
Each term must have the same non-repeated indices.

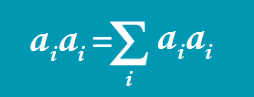
I see you are a bit perplexed by reading the theory. I agree that Einstein gives us headaches all the time, but do not worry, you will see how this equation works as magic in our code problems. Let’s discuss its Numpy function and then we will jump into some interesting examples.

The numpy.einsum() Function

The numpy.einsum() function performs the Einstein summation on the provided input. Matrix multiplication of multidimensional arrays is made easy using this function. Let’s discuss it in detail.

Syntax:

numpy.einsum(subscripts, *operands)

Parameters:

Here is what each parameter in the given syntax means:

subscripts: This is a string which is used to specify the operation.
operands: This is the collection of arrays you want to operate on.

Return Value:

This method returns Einstein’s summation convention for the operand arrays according to the provided subscripts.

Working of numpy.einsum

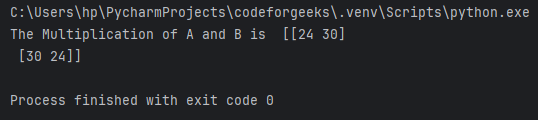
Let us understand the workings of numpy.einsum() function with an example. Consider that there are two arrays A and B and we need to multiply them.

import numpy as np

A = np.array([[4, 2], [2, 4]])
B = np.array([[3, 6], [6, 3]])

result = np.einsum('ij,jk->ik', A, B)
print("The Multiplication of A and B is ",result)

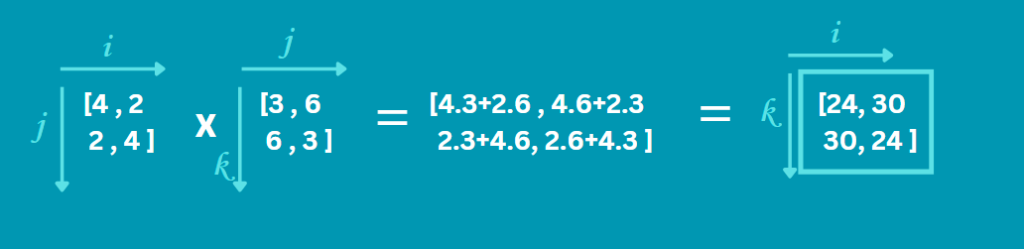
In the line ij,jk->ik, ij represents the axes of the array A, where i is for the rows and j is for the columns. jk represent the axes of array B, where j is for the rows and k is for the columns. We see that j is being repeated, which means that rows of A are being multiplied by columns of B, and since j is not included in the output, it means the product obtained is summed up. And output will be in the form of a 2D array, i.e., ik. This is how we obtain the matrix multiplication of two arrays and the output clearly justifies it:

Practical Use Cases of numpy.einsum

Now that we know that einsum helps us to find matrix multiplication with ease, it is not the only thing that einsum helps us with, it can be used in various ways. Anything that involves combinations of multiplying and summing axes can be written using einsum. Let’s see how.

Example 1:

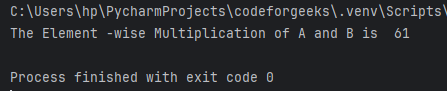
We can find out the element-wise multiplication of two array inputs. This is how einsum helps us with it.

import numpy as np

A = np.array([4, 4, 4])
B = np.array([2 ,2 ,2])

result = np.einsum('i,i->i', A, B)
print("The Element -wise Multiplication of A and B is ", result)

In this case, ‘i,i->i’ means that we take elements of index ‘i’ (rows) from array A. Similarly, we take elements from array B in the same fashion, as it is also labeled ‘i’. Then, we multiply the corresponding elements together to obtain the result.

Also, learn how to compute the product of a 1-D array in Python by clicking here.

Example 2:

If we need to calculate the dot product, we can use einsum in this way:

import numpy as np

A = np.array([4, 3, 2])
B = np.array([6 ,7 ,8])

result = np.einsum('i,i->', A, B)
print("The Dot product of A and B is ", result)

Here, ‘i,i->’ means that from both array A and array B, we take row elements labelled as i and multiply the corresponding elements together. But, instead of keeping each individual result, just sum them up. Therefore, we get the dot product.

Example 3:

Einsum can also be used to find the sum of the main diagonal. Here is the code where we find the sum of diagonal elements using einsum:

import numpy as np

A = np.array([[4, 1, 1],
           [2, 4, 2],
           [5, 5, 4]])

result = np.einsum('ii', A)
print("The sum of diagonal elements of A is ", result)

In this code, ‘ii‘ means we select and sum only the elements that have the same indices for both rows and columns, which is nothing but the diagonal elements, hence the function returns the sum of all diagonal elements.

Conclusion

I hope this article clears your mind about Einstein summation in Python. The numpy.einsum() function simplifies array and tensor calculations, making operations like matrix multiplication, dot products, and diagonal sums easy to perform. With practical examples, you can now use this function to speed up your numerical computations.

Do you know how to find the cumulative sum of a number in Python? Read here