numpy.gcd() in Python: Finding the GCD of Arrays

The gcd function in NumPy is used to calculate the greatest common divisor of numbers in arrays (GCD). It is used to facilitate fractions and solve many mathematical problems. Without this function, discovering the GCD would take longer and be more error-prone, particularly when dealing with large datasets. After reading this article, you will know about this function, its algorithm, syntax, and working along with some code examples. So let’s get started.

How to Find the GCD?

We can find the GCD of any pair of numbers using a basic algorithm called the Euclidean algorithm. Euclidean algorithm is a method to find the largest number that can divide two other numbers without leaving a remainder.

Think of two numbers, say 21 and 49. Now, find the largest number that can divide both of them without leaving a remainder. This number is called the Greatest Common Divisor (GCD).

Here are the steps of how this algorithm works on these two numbers:

Divide: We start by dividing the bigger number by the smaller one. For 49 ÷ 21, we get 2 with a remainder of 7.
Check the remainder: If the remainder is zero, we’re done! But since it’s 7, we move to the next step.
Update: Now, we replace the bigger number with the smaller one, and the smaller number with the remainder. So, a = 21 and b = 7.
Repeat: Divide 21 by 7. We get 3 with no remainder. So, the GCD is the last non-zero remainder, which is 7.

Also, if you are curious about how to find remainders using NumPy in Python, check out – numpy.remainder()

Introducing numpy.gcd

It was important to understand the Euclidean algorithm before introducing the function because now that it is clear, let us understand this NumPy function.

Syntax:

The root syntax of numpy.gcd function looks like this:

numpy.gcd(a,b)

a and b can be either single numbers or arrays. They represent the numbers for which you want to find the GCD. The return value of this function is the greatest common divisor according to the provided input value.

Working:

The function uses the Euclidean algorithm with a ‘while‘ loop. It keeps finding the remainder when a is divided by b and updates the values of a and b until b becomes zero. When b reaches zero, a holds the greatest common divisor (GCD).

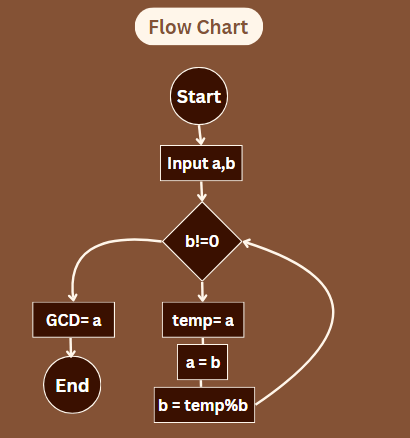
Here is the stepwise working:

Initialization: We begin by setting up the function and giving it two numbers or arrays, a and b.
Loop: We use a while loop to do the Euclidean algorithm for finding the GCD. This method keeps finding the remainder when we divide a by b until b reaches zero.
Update: Each time we go through the loop, we change the value of a to be what b was, and b to be the remainder when a is divided by b.
Result: When b becomes zero, the last value of a that isn’t zero is the GCD. We give back this number.

If a and b are single numbers, it gives the highest common factor of those two. If they are arrays, it calculates the highest common factor for each pair of numbers in the arrays.

Examples of numpy.gcd in Python

Let’s gain a better understanding of numpy.gcd function with a bunch of examples.

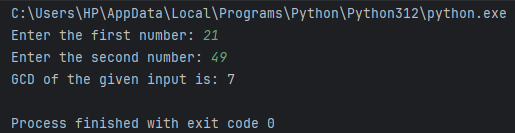
Example 1: First, let’s test this function with scalar values.

import numpy as np

a = int(input("Enter the first number: "))
b = int(input("Enter the second number: "))

print("GCD of the given input is:", np.gcd(a,b))

This code finds the GCD of two numbers. It asks the user to enter two numbers and then prints GCD.

Output:

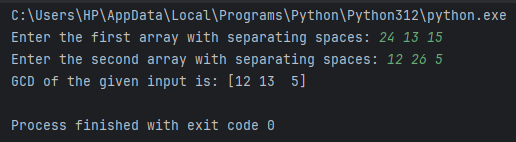
Example 2: Now let’s provide the array input.

import numpy as np

a_input = input("Enter the first array with separating spaces: ")
arr1 = np.array([int(x) for x in a_input.split()])

b_input = input("Enter the second array with separating spaces: ")
arr2 = np.array([int(x) for x in b_input.split()])

print("GCD of the given input is:", np.gcd(arr1, arr2))

Output:

It will return an array containing the GCDs when comparing the elements at the same index. When comparing 24 and 12, we get 12, when comparing 13 and 26, we get 13, and so on.

Example 3: Let’s provide huge numbers and see if it works.

import numpy as np

a = int(input("Enter the first number: "))
b = int(input("Enter the second number: "))

print("GCD of the given input is:", np.gcd(a,b))

Output:

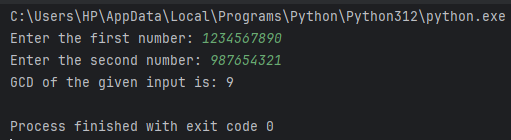
And it works! This code proves that this function can handle huge sets of data efficiently.

Summary

The numpy.gcd() in Python is used to calculate the greatest common divisor of numbers present at the same index in the given arrays. In this article, we learned how to find the GCD of numbers, and discussed the numpy.gcd() function in detail, and covered its syntax and parameters. Additionally, we went through some good examples for better understanding. We hope you enjoy our content.

You may continue your learning by reading how can you calculate cumulative sum with Numpy in Python.