numpy.unwrap() in Python: For Correcting Phase Wraparound

Phase wraparound is the instantaneous transition in phase values. This is as a result of converting the phase to fit within -π and π. In this case, when it passes above or below these limits, the phase wraps around to remain within them. To restore precision in signal processing, these jumps must be resolved. One way of solving this problem is using numpy.unwrap which is a function from NumPy.

What is Phase Wraparound?

This refers to abrupt jumps that are caused by exceeding the normal range in measuring phases. For example, if the phase ranges between 0 and 2π, any increase beyond that would wrap back around to 0 causing a discontinuity. Applications like communication systems and radar may have errors if indeed they rely on the smoothness of phase data.

Consider for example how phase wraparound can lead to wrong readings about an object’s position or motion in detecting radar systems. Removing the wraparound guarantees that phase data changes smoothly.

Introducing numpy.unwrap

The problem of phase wraparound can be solved by using the unwrap() function from NumPy which smoothens the phase data and corrects the jumps.

Syntax:

numpy.unwrap(p, discont=pi, axis=-1)

This is what each parameter means:

p: The input phase values array.
discont: This value is a threshold for detecting discontinuities and its default value is pi.
axis: This is the axis through which we are unwrapping along and by default is the last axis.

Working:

The unwrap function maintains continuous phase data by identifying and repairing jumps in the data.

As an example, consider this:

import numpy as n

input_data = n.array([0, n.pi/3, n.pi, -n.pi, -n.pi/3, 0])
print(n.unwrap(input_data))

In this example, the original phase data moves from π to -π. This was identified and fixed with numpy.unwrap thereby producing continuous phase data.

Correction Output:

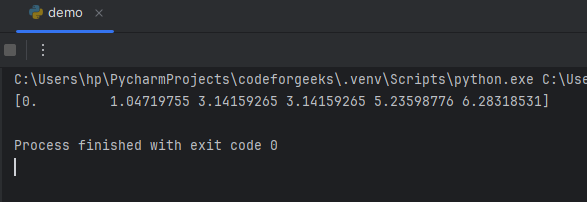
It makes sure that the phase does not jump around so much.

Examples of numpy.unwrap in Python

Now that we know the basics of how this function works, let’s go through some more examples for a better understanding.

Example 1:

Here, we will use a custom threshold (discont=np.pi/2) to handle different discontinuities.

import numpy as n

input_data = n.array([3*n.pi/2, -4*n.pi/2, 2*n.pi, 0, n.pi, -n.pi])

output_data = n.unwrap(input_data, discont=n.pi/2)

print("Here is the Original Phase Data:", input_data)
print("Here is the Unwrapped Phase Data:", output_data)

Example 2:

Here, we will unwrap phase data along the columns of a 2D array. We will keep axis=0.

import numpy as n

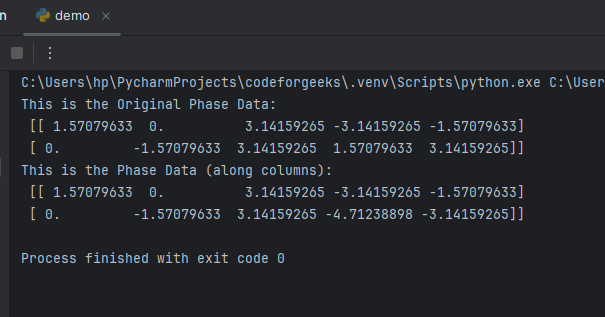
in_data = n.array([[n.pi/2, 0, n.pi, -n.pi, -n.pi/2],
                       [0, -n.pi/2, n.pi, n.pi/2, n.pi]])

out_data = n.unwrap(in_data, axis=0)

print("This is the Original Phase Data:\n", in_data)
print("This is the Phase Data (along columns):\n", out_data)

Example 3:

In this example, real-world phase data with noise is unwrapped to correct the phase continuity.

import numpy as n

n.random.seed(0)
in_data = n.linspace(0, 8*n.pi, 10) + n.random.normal(0, 0.1,10)
in_data[5:] += 4*n.pi 

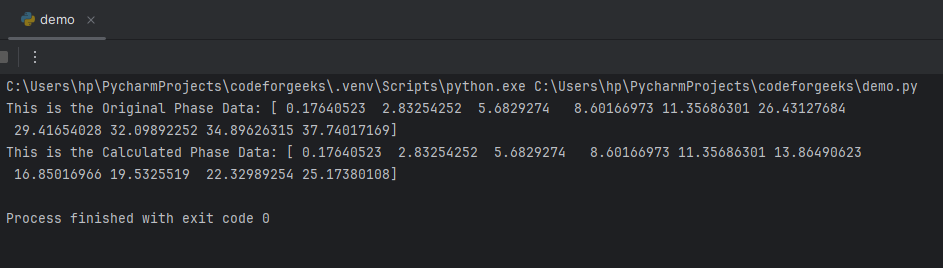
print("This is the Original Phase Data:", in_data)
print("This is the Calculated Phase Data:", n.unwrap(in_data))

Example 4:

Now we will show how to unwrap the phase of a complex signal, which is common in signal processing tasks.

import numpy as n

ls = n.linspace(0, 1, 100)
cplx_signal = n.exp(1j * (2 * n.pi * 3 * ls + n.pi/2))

in_data = n.angle(cplx_signal)
in_data[30:70] += 4*n.pi

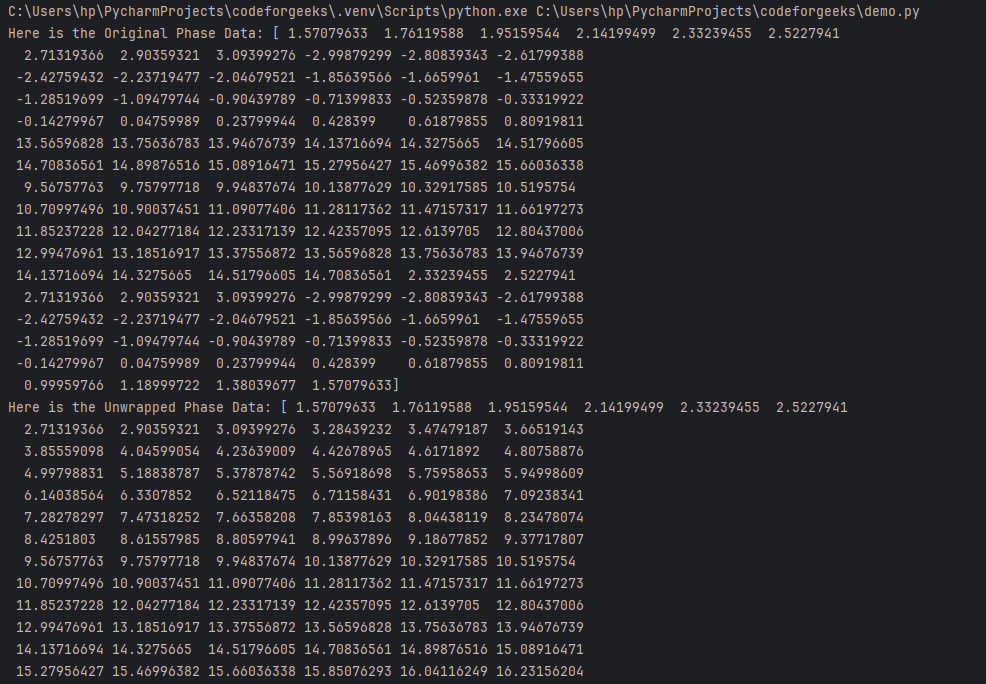
print("Here is the Original Phase Data:", in_data)
print("Here is the Unwrapped Phase Data:", n.unwrap(in_data))

Applications of Phase Wraparound

Phase wraparound affects various fields where signal processing belongs.
Radar, sonar, and communication signals cannot be adequately understood without unwrapped phases.
As far as our perception of signal behaviour goes, maintaining a continuous phase is important.
Phase information finds frequent application in communication systems where transmissions must be altered.
Misinterpretation of a wrapped result will compromise our interpretation of this transmitted signal hence affecting both transmission and reception related issues.

Conclusion

That’s it for this post. I hope you now understand what we mean by phase wraparound and how we can use the NumPy unwrap() function to address this problem in Python. We discussed the syntax, parameters, and some practical examples. Now it’s your turn to experiment with it in your own ways!

Continue Reading: