The numpy library within Python contains a wide range of functions to modify or manipulate numerical data. Amongst those is a category of functions under einsum which are noteworthy for their manipulative capabilities in handling the N-dimensional arrays. They can seamlessly support adding, multiplying or rearranging any given input arrays in very short time periods thereby catapulting the computational capabilities.
However, the name of this function might be a bit deceiving since it has nothing to do with neither the scientist, Einstein nor the mathematical operation of summing.
This article shall focus on a particular variant of einsum – the einsum_path( ) function which is used for creating intermediary arrays for evaluation of the lowest cost contraction order for the given einsum expression. This function is not limited to contracting the given input arrays into those with similar dimensions. Rather, it goes the extra mile to perform the contraction for a different dimension of the resulting array.
Syntax of einsum_path( ) Function
Given below is the syntax of the einsum_path( ) function detailed with its basic components that are required for its effective functioning.
Syntax:
numpy.einsum_path(subscripts, *operands, optimize = ‘greedy’)
Parameters:
- subscripts – used to specify the input subscripts
- *operands – used to list the input arrays
- optimize – set to ‘greedy’ by default and is used to specify how to deduce the desired path type. One can also choose to set this with the alternate option, ‘optimal’.
The difference between the two available options for the optimize is that the ‘greedy’ setting shall analyse each step before selecting the best-suited contraction pair. Whereas, the ‘optimal’ algorithm on the other hand analyses all the existing combinations in order to identify every possible path for contracting the inputs and then select the order which best fits the least cost approach. The result of the einsum_path( ) function is always in the form of a list.
Using einsum_path( ) Function in Python
We shall get things started by importing the numpy library using the following code before deploying the einsum_path( ) function.
import numpy as np
Once done, it is time to construct the input arrays that are to be subjected to the contraction as shown below.
ar1 = np.array([[10, -9], [5, -7]])
ar2 = np.array([[0, 4, 6], [7, 5, -3]])
ar3 = np.array([[-1, 4], [6, 8], [-2, 4]])
Following the inputs declaration, one shall now summon the einsum_path( ) function using the code below.
pt = np.einsum_path('ij, jk, ki -> ii', ar1, ar2, ar3, optimize = 'greedy')
The logic behind the execution of the above code is to contract the inputs ar2 and ar3 initially and then use the corresponding results for deducing the final contraction.
print(pt[0])
print(pt[1])
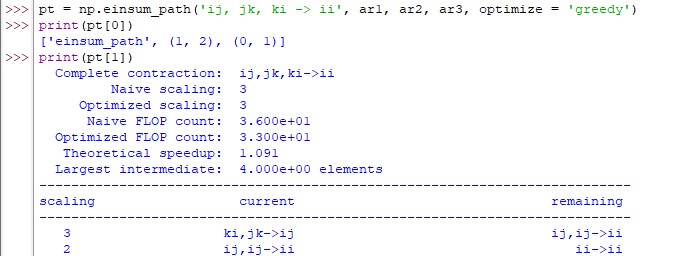
The above code demonstrates the working of the ‘greedy’ setting. So, let us now have a look at what ‘optimal’ setting has got to offer.
pt = np.einsum_path('ij, jk, ki -> ii', ar1, ar2, ar3, optimize = 'optimal')
print(pt[0])
print(pt[1])
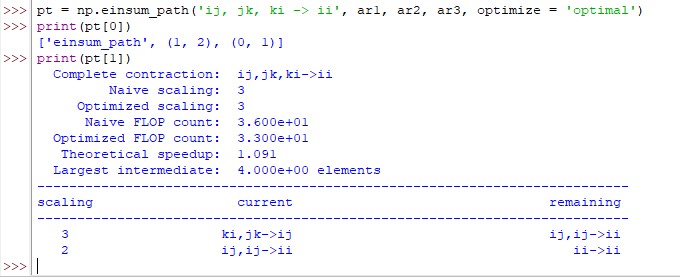
It could be observed that the results returned by both settings are similar. This could be explained by the simplicity of the inputs that we have used for the demonstration purpose. Nevertheless, one has to bear in mind that when the inputs fed become complex, then the computation time with the ‘optimal’ algorithm would always be greater than that incurred by the ‘greedy’ algorithm. So, know your requirements and choose wisely.
Conclusion
Now that we have reached the end of this article, hope it has elaborated on the procedure to put into use, the einsum_path( ) function in Python. Here’s another article that elaborates on calculating the outer product of vectors using the outer( ) function from the numpy library in Python. There are numerous other enjoyable and equally informative articles in CodeforGeek that might be of great help to those who are looking to level up in Python.
Reference
https://numpy.org/doc/stable/reference/generated/numpy.einsum_path.html





