Vectors play an important role in the field of mathematics for helping with the navigation around different spaces & planes. This article shall set out to explore one of the many functions that can be carried out with vectors in Python programming – the outer( ) function from the numpy library.
Before that let us set things off by importing the numpy library using the below code:
import numpy as np
The nuances of the outer( ) function shall be covered in each of the following sections:
- Syntax of outer( ) Function
- Using outer( ) function in One Dimensional Arrays
- Using outer( ) function in N-Dimensional Arrays
- Using outer( ) function with Letters
- Using outer( ) function with other Numpy Functions
Syntax of outer( ) Function
The outer product of any given set of vectors is determined by multiplying each element in one vector with the corresponding element in the other and then forming the resultant vector using each value from the result obtained. Given below is the syntax of the outer( ) function.
Syntax:
numpy.outer(a, b, out=None)
Parameters:
- a – n-dimensional array set as the first input vector
- b – n-dimensional array set as the second input vector
- out – an optional construct set to none by default, but could be used to store the results in an array that is of the same length as that of the result
Using outer( ) Function in One-Dimensional Arrays
Let us create a couple of one-dimensional arrays as shown below to find their outer product.
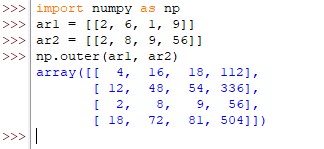
ar1 = [[12, 36, 71, 99]]
ar2 = [[2, 8, 9, 56]]
np.outer(ar1, ar2)
The resulting output would have a similar number of columns, but the striking difference would be that of the rows, which in this case shall be 4 instead of 1.
To understand this further, let us drill down a bit. The first element of the first array, ‘12’ is multiplied with the entire first row of the second array, one element after the other. All the results form the first row of the output array.
This process loops over and over until it reaches the last element of the array. Once done, the process gets repeated for the second element of the first array and so on and so forth.
Output:
Using outer( ) Function in N-Dimensional Arrays
In this section, we shall calculate the outer product of vectors using input arrays which are constructed with 2 rows and 3 columns. Let us run the code to have a look at what the results might be!
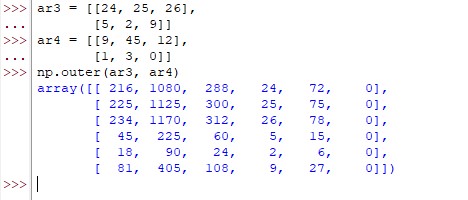
ar3 = [[24, 25, 26],
[5, 2, 9]]
ar4 = [[6, 8, 12],
[4, 3, 10]]
np.outer(ar3, ar4)
3 times 2 gives us 6 and so does the size of the output array – it is a 6×6.
Output:
Using outer( ) Function with Letters
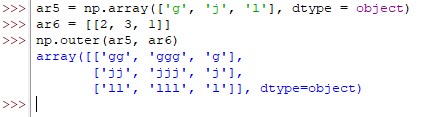
Multiplying numbers is not only the capability of the outer( ) function but one can also apply the function to arrays with alphabets, but the catch here is the datatype that is to be set to make it happen. Set the dtype as ‘object’ as shown below & the letters in the array are in for a ride to replicate.
ar5 = np.array(['g', 'j', 'l'], dtype = object)
ar6 = [[2, 3, 1]]
np.outer(ar5, ar6)
Given below is the output when the above code is run.
Output:
Using outer( ) Function with Numpy Functions
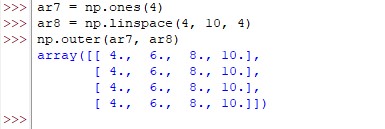
The outer( ) function also works well with other functions within the numpy library such as ones( ) and the linspace( ). In this section, we shall deploy the linspace( ) function to divide the range between 4 & 10 into four parts and then apply the outer( ) function.
ar7 = np.ones(4)
ar8 = np.linspace(4, 10, 4)
np.outer(ar7, ar8)
Output:
Conclusion
Now that we have reached the end of this article, hope it has elaborated on how to use the outer( ) function from the numpy library. Here’s another article that explains what are docstrings and how to use them effectively in Python. There are numerous other enjoyable and equally informative articles in CodeforGeek that might be of great help to those who are looking to level up in Python.
Reference
https://numpy.org/doc/stable/reference/generated/numpy.outer.html

