Roll the calendar a few centuries back until you land in 1817. It was the very same year that a German who was an astronomer by profession was taking a close look at the planetary movements in space. Known by the name, Friedrich Wilhelm Bessel he went on to refer to the magnum opus of the greatest astronomer of his time – Kepler’s equations on the planetary motions!
Delving deeper into the investigation of Kepler’s equations, it was not long before he came to know that he had deduced something new.
This deduction of his, when expressed mathematically would result in an equation that could successfully explain the fluid motion around a cylinder. That right there was the birth of the Bessel’s equation.
In the forthcoming years, the very same equation shall be widely adopted for providing solutions to the problems involving:
- Heat flow in a solid cylinder
- Electric current flow in a solid cylinder
- Motion of electromagnetic waves around a wire
- Deformation in an elastic body
The Bessel’s Equation:
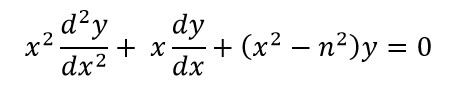
Solving the above differential equation results in the Bessel’s function. But who has the time to solve and trace through each step to get to Bessel’s function in these restless times? Thus, we revert to Python, which saves us from misery by directly taking us to the results. This is done with the aid of an exclusive function – the numpy.i0 (i-zero; not ‘o’). What this means is it is the Bessel’s function which is of the order zero.
This article shall elaborate on the usage of the i0( ) function from the numpy library of Python through each of the following sections:
- Syntax of numpy.i0( ) Function
- Deploying numpy.i0( ) on N-Dimensional Arrays
- Plotting numpy.i0( ) Results
Let us get things started by importing the numpy library using the following code:
import numpy as np
Syntax of numpy.i0( ) Function
Unlike most other functions, this one has a pretty simple syntax as given below. The Bessel’s function of the first kind, order zero is denoted by I0 in mathematics.
Syntax:
numpy.i0(x)
where x is InputScalar or N-dimensional array.
Deploying numpy.i0( ) on N-Dimensional Arrays
Let a 4×1 array be constructed for usage against the i0( ) function.
ar1 = np.array([[2, 8, -3, 4]])
np.i0(ar1)

Upon observing the above results, one can very well identify that the results in the output array are of the same dimensions as the input array ‘ar1’. Thereby, each element in the resultant array is the value given by the Bessel’s function upon processing the respective value from the input array.
However, it is to be noted that the i0( ) function would throw errors when used against complex numbers as shown below.
ar2= np.array([4, -18j])
np.i0(ar2)
Output:
TypeError: i0 not supported for complex values
Plotting numpy.i0( ) Results
It does not become a complete package until the results of a mathematical function are plotted on a graph and so shall be done for the i0( ) function too in this section. But before that, it would be needed to access some entities from another library in Python – the matplotlib library, using the following code.
import matplotlib.pyplot as plt
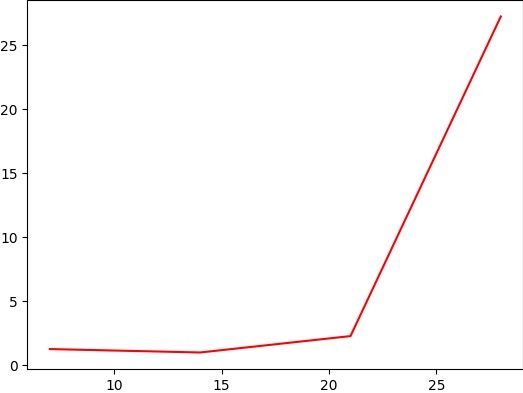
After that, we shall use the results of the ar1 as the coordinates for the plot.
ar1 = np.array([[-1, 0, 2, 5]])
r1 = np.i0(ar1)
Now let us plot the results against the x-axis in red using the below code.
x = np.arange(0, 28, 7)
plt.plot(x, r1, 'r')
Output:
Conclusion
Now that we have reached the end of this article, hope it has elaborated on how to use the i0( ) function from the numpy library. Here’s another article that details how to find the vector dot product using the vdot( ) function from the numpy library in Python. There are numerous other enjoyable and equally informative articles in CodeforGeek that might be of great help to those who are looking to level up in Python.
Reference
https://numpy.org/doc/stable/reference/generated/numpy.i0.html





