numpy.vdot() in Python: Calculating Vector Dot Product

The physical entities that are used to represent both the magnitude and direction in the direction of movement of any particular object are known as vectors. Primarily being deployed for finding the way around different spatial planes, they do play a crucial role in mathematics.

Despite the number of operations that can be done using the vectors, this article shall focus on exploring a built-in function within the numpy library that is used to determine the dot product of any given vectors.

The vdot() function shall be summoned from the numpy library to serve the very purpose. So, let us get started by importing the numpy library using the code given below.

import numpy as np

Once done, the vdot( ) function shall be explored in detail through each of the below listed sections:

Introduction to vdot( ) function
Syntax of vdot( ) function
Using vdot( ) function for N-Dimensional Arrays
Using vdot( ) function for Complex Numbers

Introduction to vdot( ) Function

When there is already a dot( ) function to determine the dot product, why on Earth do we have a vdot( ) function in the first place?

I too used to have this question, for which I did a deep dive to notice an intricate difference between these two. At face value, both might be the same, but they certainly are not!

Should the inputs given contain entities that are complex numbers, the vdot( ) function makes use of the technique known as complex conjugate by which it uses the complex conjugate of the first input and determines the vector dot product of the input vectors. But, where both these functions stand apart is when the N-dimensional arrays are being used.

When the dot( ) function fancies the usage of simple matrix multiplication to determine the dot product of the given N-dimensional arrays, the vdot( ) function kicks things off by transforming the input N-dimensional arrays by flattening them into their 1-D equivalents and then proceeds with calculating the dot product.

Syntax of vdot( ) Function

Given below is the syntax of the vdot( ) function.

numpy.vdot(a, b)

where,

a – Complex number or N-dimensional array which is the first input vector
b – Complex number or N-dimensional array which is the second input vector

Using vdot( ) Function for N-Dimensional Arrays

Let us declare the desired vectors in the form of arrays to get started with calculating the vector dot product.

Example:

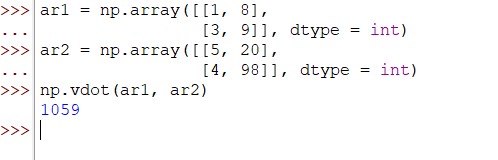
ar1 = np.array([[1, 8],
                [3, 9]], dtype = int)
ar2 = np.array([[5, 20],
                [4, 98]], dtype = int)
np.vdot(ar1, ar2)

Executing the above code results in the following computation to determine the vector dot product of the two inputs.

The first element of the first input array is multiplied with the first element of the second input array, such as ‘1×5’. The same is done for the subsequent elements until the last element of both inputs are multiplied.
Then, the results of each of these products are added together to deduce the vector dot product of the input N-dimensional arrays. (1×5)+(8×20)+(3×4)+(9×98) = 1059.

Output:

Vector Dot Product Of Two N Dimensional Arrays — Vector Dot Product of Two N-Dimensional Arrays

Using vdot( ) Function for Complex Numbers

The vdot( ) function uses the same technique as stated in the previous method for N-dimensional arrays for finding the vector dot product with two complex numbers as inputs. But there shall be an additional step which is exclusive when the complex numbers are involved which is to multiply their conjugate for deducing the final result.

Example:

ar3 = [[4+3j, 6-98j]]
ar4 = [[2-35j, 8+28j]]
np.vdot(ar3, ar4)

Output:

Vector Dot Product For Complex Numbers — Vector Dot Product for Complex Numbers

Conclusion

Now that we have reached the end of this article, hope it has elaborated on the usage of vdot( ) function from the numpy library for determining the vector dot product. Here’s another article that can be your comprehensive guide to using Statements in Python. There are numerous other enjoyable and equally informative articles in CodeforGeek that might be of great help to those who are looking to level up in Python. Whilst you enjoy those, hasta luego!