numpy.logaddexp() in Python: An Easy Guide

Hello Geeks! Welcome to another guide where we will explore an interesting mathematical concept: the logarithm of the sum of exponentials. Sounds new, right? You will be surprised to know that a separate function is dedicated to calculating it in NumPy, which is called logaddexp(). In this article, we will discuss everything from the basic usage of this function to its syntax, functioning, and examples. Let’s get started.

Understanding Logarithm of Sum of Exponentials

This concept means that we take the exponentials of input numbers, sum them up, and then find the natural logarithm of the result.

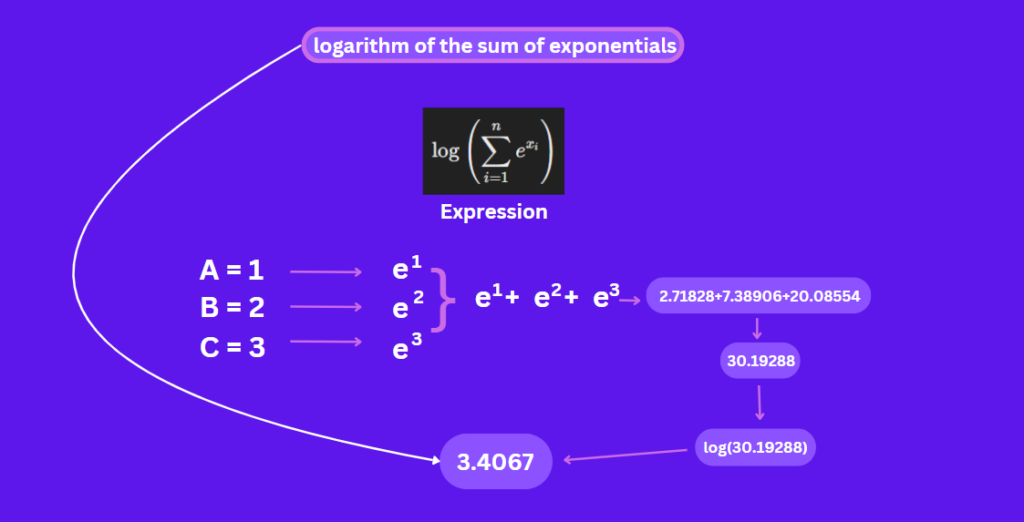
Suppose we have a set of numbers: A=1, B=2, and C=3. Now, let’s calculate the sum of exponentials of these numbers:

Firstly, we will take the exponents of these numbers, sum up their values, and then take the natural logarithm of this sum.

So, the logarithm of the sum of exponentials of 1,2,3 is approximately 3.40673.4067.

This idea helps a lot in statistics, especially with probabilities. It comes up often when we are dealing with numbers that grow fast, like in certain functions used in neural networks, or when figuring out how likely something is in maximum likelihood estimation.

Introducing numpy.logaddexp

The Numpy logaddexp simplifies adding probabilities in log space to prevent numerical issues like underflow or overflow by calculating the logarithm of the sum of exponentials of the inputs.

Syntax:

The syntax of this function looks something like this:

numpy.logaddexp(x1, x2, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj])

Let’s see what each parameter means:

x1, x2: Numbers or lists of numbers. These are the values we are using to find the logarithm of the sum of their exponentials.
out (optional): Where the result goes. If given, it must match the shape of the inputs. If not, a new array is made.
where (optional): A condition that decides where the result is stored. If true, it goes to the out array, otherwise, the out array keeps its original value.
Other options like casting, order, dtype, and subok control how the calculations are done and the type of the result.

Working:

It takes two arrays or values as input.
Calculates the exponential of each input.
Sums up the exponentials.
Takes the logarithm of the result.
Returns the logarithm of the sum of exponentials.

Examples of numpy.logaddexp in Python

This concept is quite difficult so let’s simplify it with some examples to develop a clear understanding and see how to use it in Python code.

Example 1:

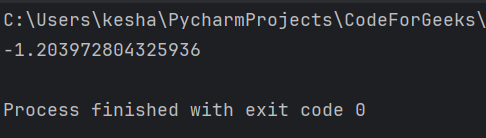
Let’s start with a basic implementation using scalar values.

import numpy as np

a = np.log(0.1)
b = np.log(0.2)

result = np.logaddexp(a, b)
print(result)

In this example, we calculate the logarithm of the sum of exponentials of a and b.

Example 2:

We can calculate the logarithm of the sum of exponentials with desired conditions using the “where” parameter.

import numpy as np

a = np.array([2, 4, 6])
b = np.array([3, 5, 7])
condition = (b > a)

result = np.logaddexp(a, b, where=condition)
print(result)

Example 3:

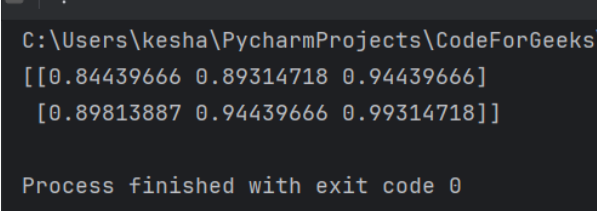
Calculating the logarithm of the sum of exponentials with broadcasting is also possible. Let’s see how:

import numpy as np

x = np.array([0.1, 0.2, 0.3])
y = np.array([0.2, 0.3])

result = np.logaddexp(x, y[:, np.newaxis])
print(result)

First, let’s learn what we mean by broadcasting. Broadcasting is a property that allows us to use arrays of different shapes together in an arithmetic operation. Generally, during these operations, Numpy compares the shapes of the arrays element-wise. It trails from right to left, it proceeds with the calculation only if the shape matches, or else it throws a value error.

In this code, y[:, np.newaxis] changes the (2) shape to the (2,1) shape as it adds a new axis. Also, we know that the shape of x is (3), and due to broadcasting, Numpy will extend the dimensions of x on its own to make it a (3,1) shape. Now, both arrays have compatible shapes for element-wise operation. Hence, the result will be generated without any errors.

Summary

And that’s it for this article. We hope that you are clear with the idea of the logarithm of the sum of exponentials. It is a fresh concept that we got to know about. We went through its theory and implementation of numpy.logaddexp() function in Python and also covered some useful examples. Numpy provides us with more such methods for logarithmic operations, if you’re getting into that, check out Log1p(), Log2(), and Log10().