The Numpy library is considered the most important and widely used library for numerical computing. NumPy affords a powerful array processing functionality and helps a huge range of mathematical capabilities, making it an essential tool for data manipulation and evaluation. Among the many features that NumPy offers, broadcasting stands out as a unique and powerful concept that simplifies array operations and enhances the code’s efficiency. We will get the knowledge of NumPy broadcasting, explaining its core principles, and demonstrating its utility with code examples.
Introduction to NumPy Arrays
NumPy( Numerical Python), is an open-source Python library that serves massive, multi-dimensional arrays and matrices. Developed in 2005 via Travis Oliphant, NumPy is the foundation for lots of other libraries in Python programming.
The Numpy library provides you with the Numpy arrays which is a multidimensional container that is used for storing homogenous data. This means that each element in a NumPy array should have the same data type because it provides you with optimized memory and perform faster calculation. NumPy arrays are more efficient for numerical operations than standard Python lists due to their contiguous memory layout.
Creating NumPy Arrays:
To create a NumPy array, you can make of numpy.array() function, this function requires a list and tuple as an argument.
import numpy as np
arr = np.array([3,4,5])
This will create an array that holds the value [3,4,5] and we can further perform some mathematical operations to manipulate and change the array.
Array Attributes:
NumPy arrays come with several attributes that provide valuable information about the array. Some common attributes include shape, dtype, and size. For instance:
import numpy as np
arr = np.array([1,2,4])
print(arr.shape) # Output: (3,)
print(arr.dtype) # Output: int32
print(arr.size) # Output: 3
- shape: This indicates the shape of the Numpy array. For a one-dimensional array like arr, the form is represented as a tuple containing the number of elements alongside each axis. In this example, the tuple (3,) method that the array arr has three elements alongside the primary axis
- dtype: This indicates the data type of the elements in the NumPy array arr.
- size: It indicates the no of elements in an array
Indexing and Slicing Arrays:
You can access elements in a NumPy array using square brackets and indices. Additionally, you can perform slicing operations to extract specific portions of the array. Here’s an example:
import numpy as np
arr = np.array([5,6,7,8,9])
print(arr[0]) # Output: 5
print(arr[1:4]) # Output: [6 7 8]
print(arr[::-1]) # Output: [9 8 7 6 5]
Broadcasting NumPy Arrays
Numpy broadcasting is an effective function within the NumPy library, which lets arrays of different shapes be changed, manipulated, or operated upon with mathematics operations without the need for an explicit element-wise loop(for and while loop). This broadcasting behaviour is especially useful while dealing with arrays of various dimensions because it facilitates to avoid unnecessary memory duplication and improves computational efficiency.
When performing arithmetic operations or other element-wise operations on arrays with exclusive and different shapes, NumPy automatically broadcast the smaller array to match the shape of the larger array, making the operation viable. Broadcasting follows a set of guidelines to decide how arrays with specific shapes may be aligned and combined. These regulations ensure that the size of the arrays are compatible and that the elements are operated upon in a meaningful way. By using broadcasting, NumPy provide cleaner and greater concise code while keeping efficient memory usage and optimized performance. Overall, NumPy broadcasting significantly simplifies array operations and complements the library’s power and ease of use.
Broadcasting with Scalar
Broadcasting with scalar is one essential feature of Numpy broadcasting. In this when you apply any arithmetic operation between a scalar value (single value) and an array, then the Numpy broadcast changes the shape of the scalar as same as of array. This allows you to apply any arithmetic operation between two without creating a new array with the same size as the original array provided.
Example:
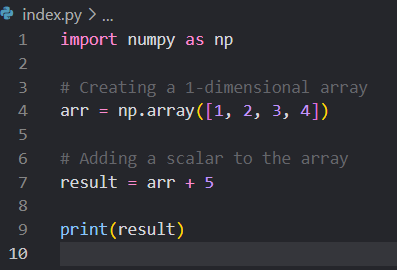
In this example, we have a 1-dimensional array arr with shape (4). When we add scalar 5 to the array, broadcasting comes into play. The scalar is broadcasted to the shape of the array, and element-wise addition is performed which means for each element 5 is added.
Output:
[6 7 8 9].
Broadcasting Between Two Arrays
The broadcasting process involves comparing the dimensions of the arrays, starting from the last axis, and determining if they are compatible with broadcasting based on specific rules. If the dimensions along an axis are the same for both arrays or one of them has size 1 along that axis, they are considered compatible for broadcasting. The smaller array is then implicitly duplicated or stretched along the corresponding dimensions to match the shape of the larger array, enabling element-wise operations to be carried out efficiently.
Example:
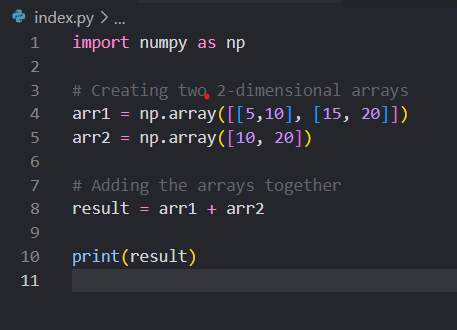
In the above case, we have two arrays, arr1 and arr2. Since broadcasting is possible, NumPy duplicates the elements of arr2 along the second dimension to match the shape of arr1. The broadcasting effectively creates a 2×2 array from arr2 with elements [10, 20] in both rows.
Then, element-wise addition is performed for example [[ 5 + 10, 10 + 20],
[15 + 10, 20 + 20]]
Output:
[[15 30] [25 40]]
Broadcasting Between 1-D and 2-D Arrays
Broadcasting between 1-Dimensional and 2-Dimensional arrays is a common scenario in array operations. When performing element-wise operations among these arrays, broadcasting expands the 1-D array or broadcasted to match the shape of the 2-D array due to which operation between them can be held smoothly. The broadcasting rules come into play right here, wherein the dimensions of both arrays are compared starting from the last axis and checked for compatibility. If the dimensions along an axis are the same for both arrays or one of them has size 1 along that axis, they are considered compatible for broadcasting
Example:
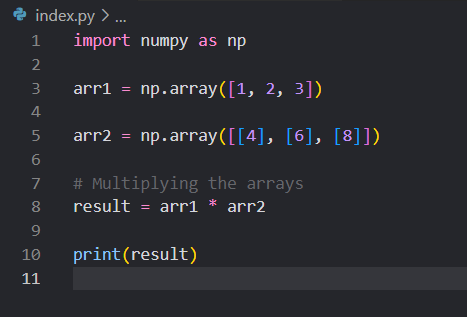
Here, we have a 1-D array arr1 and a 2-D array arr2. Broadcasting allows these arrays to be broadcasted to a common shape (3, 3). Element-wise multiplication is then performed between the arrays.
Output:
[[ 4 8 12][ 6 12 18][ 8 16 24]]
Broadcasting Between Incompatible Shapes
In this case, you will look into the case when the two arrays are not compatible with each other which means you can not broadcast one array to another array then you can handle the error using the try-catch block or any error handling methods.
Example:
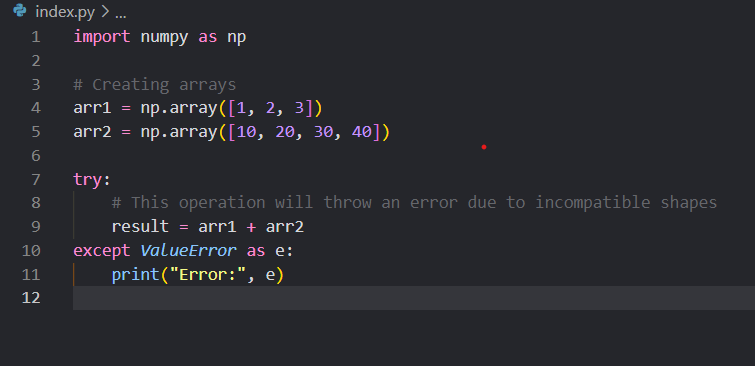
In this example, we have two arrays, arr1 with shape (3,) and arr2 with shape (4,), and they have incompatible shapes for broadcasting. As a result, when we try to add them together, a ValueError is raised with the below message.
Output:
operands could not be broadcast together with shapes (3,) (4,)
Advantage of Numpy Broadcasting Over Traditional Methods
Let us now take a look at the advantages of Numpy broadcasting over traditional methods.
1. Element-Wise Operations
Numpy broadcasting allows performing element-wise operations between arrays of different shapes. Element-wise operations mean implementing mathematical operations on the corresponding element of arrays. With broadcasting, NumPy automatically aligns the shapes of the arrays, making it possible to apply the operation efficiently. This help in many ways as you don’t require the use of explicit loops, which make the code more concise and readable.
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([10, 20, 30, 40])
result = arr1 + arr2 # Output: [11 22 33 44]
2. Memory Efficiency
Numpy broadcasting performs operations without creating new arrays, which leads to memory efficiency. Traditional methods regularly require intermediate arrays, which could consume a significant amount of memory, especially while coping with huge datasets. Broadcasting, on the other hand, operates on the arrays in place, avoiding unnecessary memory allocation. This efficiency becomes crucial when working with large-scale data, as it helps to minimize memory usage and potential slowdowns.
3. Performance Improvements
Numpy broadcasting is an effective feature that takes the benefit of optimized C and Fortran code behind the curtain, which enhances its performance compared to standard methods of array manipulation in Python. When acting operations with NumPy arrays, the broadcasting mechanism effectively aligns arrays of various shapes without the need for specific loops, making it feasible to process massive or multidimensional arrays a lot quicker.
In traditional Python programming, when running with arrays, developers regularly must use loops to carry out element-wise operations among arrays of various shapes. These loops can be sluggish and less efficient, especially while handling huge datasets, as they lack the optimized low-level language implementations that Numpy Broadcasting utilizes.
4. Code Simplicity
Broadcasting simplifies the code structure by eliminating the need for explicit loops and additional conditional checks for array shapes. With broadcasting, developers can focus on the logic of mathematical operations rather than dealing with the complexities of handling array shapes. This help to achieve the desired outcome more swiftly and reduce the complicated backend operations.
Summary
In conclusion, Numpy Broadcasting is a game-changer when it comes to element-wise operations on arrays of different shapes. Its ability to handle arrays with varying dimensions efficiently and effectively makes it a must-have tool for any Python programmer dealing with numerical computations.
So go ahead and leverage the power of Numpy Broadcasting in your projects to write cleaner, more concise, and memory-efficient code!!!
RECOMMENDED ARTICLES:
References
- https://numpy.org/doc/stable/reference/generated/numpy.array.html
- https://numpy.org/doc/stable/user/basics.broadcasting.html





