Today, we’ll learn to solve Wines Problem using dynamic programming C++. It’s a dynamic programming problem. Dynamic programming is one of the most difficult topics of DSA. We’ll learn to solve this problem using the concept of dynamic programming. Let’s get started.
Also read: Greedy Problem Expedition Using C++
Problem Statement for Wines Problem
You own a wine shop. Your shop has N bottles of wines. The price of the wine increase as the years pass by. You have the price list of all the bottles of wine. Assume that, all the bottles are arranged linearly. You can only sell the bottle of wine either from the left end or the right end. After Y years the price of every wine bottle becomes Y times its initial price. Find the maximum profit you can make by selling all the bottles of wine.
Input Format
The input will be of the form:
N: Total number of bottles of wines
P1 P2 P3 ...... P(n-1) Pn: Prices of bottles of wines
For example,
Input:
5
2 3 5 1 4
Solution: 50
Order of selling the bottles: 1st -> 5th -> 4th -> 2nd -> 3rd
Input:
3
1 10 7
Solution: 45
Order of selling the bottles: 1st -> 3rd -> 2nd
Approach to Solving the Wines Problem
The greedy strategy will fail here. The selection of the current bottles affects the revenue of the remaining bottles.
How To Deal With Dynamic Programming Problems
Dynamic programming problems are recursive problems that require some extra aid. Similar to recursive solutions, the dynamic programming solutions compute all the subproblems of a problem.
Dynamic Programming = Recursion + Memoisation = Never solve the same problem twice
Recursion: Compute all the subproblems of a problem.
Memoisation: Store the results of expensive computations.
Pseudocode
Below is the step by step process that we’ll follow to code the solution.
- wines_profit(int wines[], int i, int j, int y, int dp[][100])
- Base Case: if no bottles are left.
- if(i > j)
- Here, i = index of the bottle from the left.
- j = index of the bottle from the right.
- Memoisation: check if the solution is already computed.
- if(dp[i][j])
- If the solution is there, return the answer.
- return dp[i][j];
- Else, compute the solution
- Compute the outcomes of both choices.
- profit = profit of current bottle + profit of remaining bottles
- If we select the bottle on the left.
- int op1 = (wines[i] * y) + winesProfit(wines, i+1, j, y+1, dp);
- Otherwise,
- int op2 = (wines[j] * y) + winesProfit(wines, i, j-1, y+1, dp);
- Store the solution.
- dp[i][j] = max(op1, op2);
- Return the answer.
- return dp[i][j];
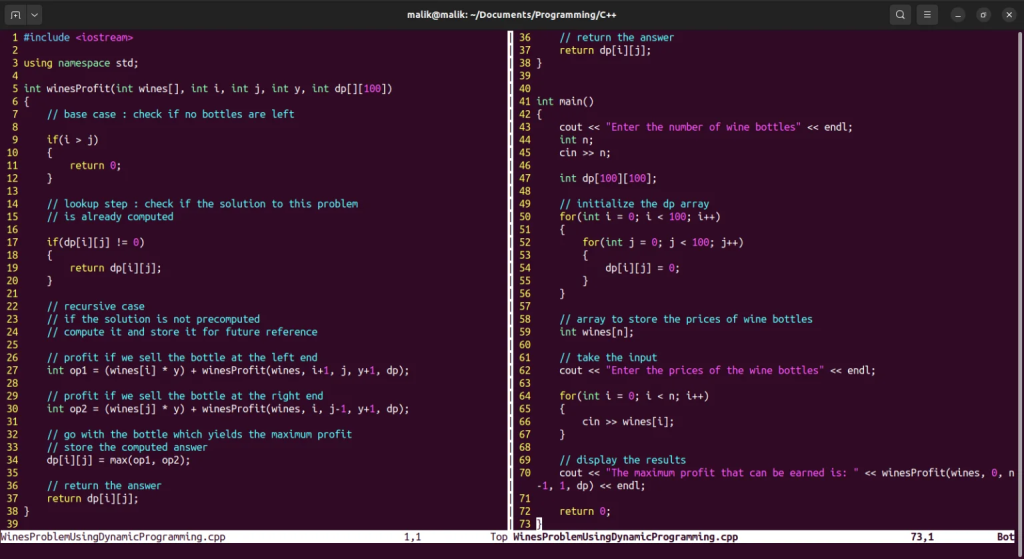
Wines Problem Using Dynamic Programming In C++ Program
#include <iostream>
using namespace std;
int winesProfit(int wines[], int i, int j, int y, int dp[][100])
{
// base case : check if no bottles are left
if(i > j)
{
return 0;
}
// lookup step : check if the solution to this problem
// is already computed
if(dp[i][j] != 0)
{
return dp[i][j];
}
// recursive case
// if the solution is not precomputed
// compute it and store it for future reference
// profit if we sell the bottle at the left end
int op1 = (wines[i] * y) + winesProfit(wines, i+1, j, y+1, dp);
// profit if we sell the bottle at the right end
int op2 = (wines[j] * y) + winesProfit(wines, i, j-1, y+1, dp);
// go with the bottle which yields the maximum profit
// store the computed answer
dp[i][j] = max(op1, op2);
// return the answer
return dp[i][j];
}
int main()
{
cout << "Enter the number of wine bottles" << endl;
int n;
cin >> n;
int dp[100][100];
// initialize the dp array
for(int i = 0; i < 100; i++)
{
for(int j = 0; j < 100; j++)
{
dp[i][j] = 0;
}
}
// array to store the prices of wine bottles
int wines[n];
// take the input
cout << "Enter the prices of the wine bottles" << endl;
for(int i = 0; i < n; i++)
{
cin >> wines[i];
}
// display the results
cout << "The maximum profit that can be earned is: " << winesProfit(wines, 0, n-1, 1, dp) << endl;
return 0;
}
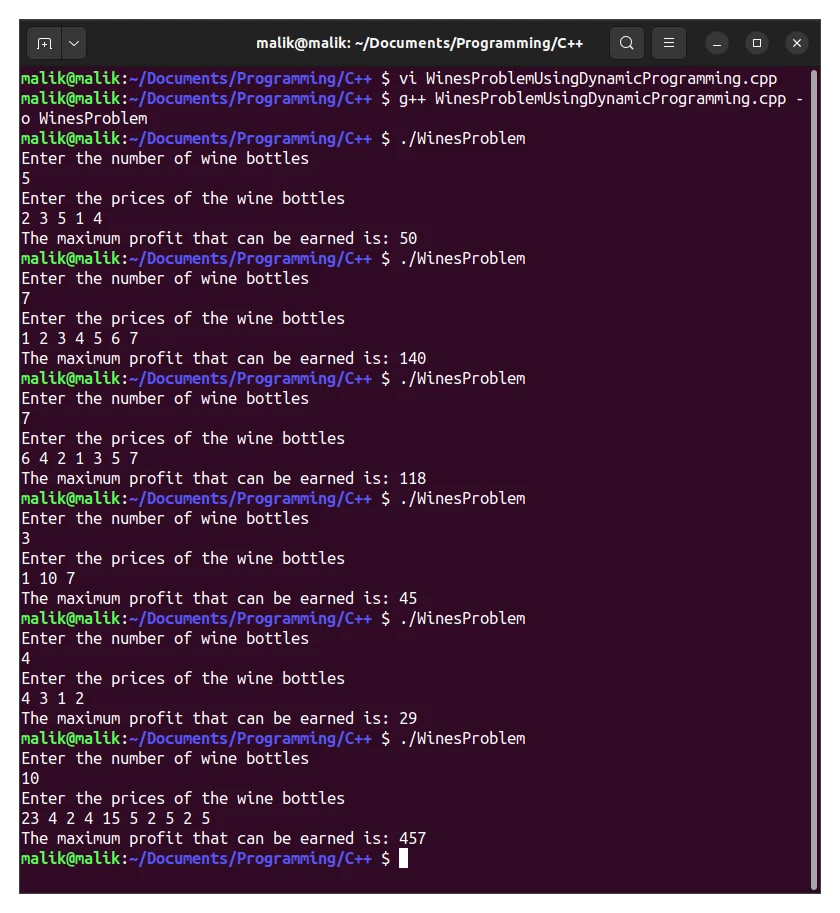
Output
Conclusion
In this article, we learned to solve the wines problem using dynamic programming in C++. We used the concept of recursion + memorization(Dynamic Programming) to solve this problem. Dynamic programming solutions are of two types. The first is the bottom-up approach and the second one is the top-down approach. In this article, we used the bottom-up approach to develop the algorithm. In the end, we implemented a C++ program to demonstrate the working of our solution. That’s all for today, thanks for reading.





