In today’s article, we’ll learn to sort linked lists using C++. Just like other data structures, there are times when we need to sort a linked list, and today we’ll see how are we gonna do that. You must be aware of the presence of multiple sorting algorithms to sort data structures.
Today we’ll implement merge sort for linked lists. Why merge sort? This is because the merge sort algorithm runs in O(Nlog2N) time complexity, which is efficient for linked lists of the size up to 106. This is going to be really interesting and learning for all, so without any further delay, let’s get started.
Also read: A Complete Guide to Linked Lists In C++
Problem Statement
Given a linked list, your task is to sort the linked list and print it. Consider the following examples/ test cases.
Input linked list:
Head <-- 5 <-- 8 <-- 6 <-- 7 <-- 10 <-- 1 <-- 4
Sorted linked list:
Head <-- 1 <-- 4 <-- 5 <-- 6 <-- 7 <-- 8 <-- 10
Input linked list:
Head <-- 54 <-- 28 <-- 61 <-- 17 <-- 104 <-- 44
Sorted linked list:
Head <-- 17 <-- 28 <-- 44 <-- 54 <-- 61 <-- 104
Input linked list:
Head <-- 4 <-- 3 <-- 2 <-- 7 <-- 10
Sorted linked list:
Head <-- 2 <-- 3 <-- 4 <-- 7 <-- 10
Input linked list:
Head <-- 50 <-- 80 <-- 60 <-- 70 <-- 100 <-- 10 <-- 40
Sorted linked list:
Head <-- 10 <-- 40 <-- 50 <-- 60 <-- 70 <-- 80 <-- 100
Concept of Sorting Linked Lists
Merge sort is a divide and conquer algorithm. It implies that we will implement the solution by breaking down the problem into various subproblems of a similar kind. We keep on repeating the same process until we hit a predefined base case. A base is a problem that we can solve using constant time and space resources. Below are the steps to merge and sort a linked list.
- Divide: Divide the linked list into two parts about its mid-point.
- Node *mid = mid_point(head);
- Now, divide point to the head by: Node *a = head;
- This pointer will point to the mid_point: Node *b = mid->next;
- To evaluate the mid-point of the linked list, use the fast and slow pointers approach.
- Sort: Sort the smaller linked lists recursively
- merge_sort(a);
- merge_sort(b);
- Merge: Merge the sorted linked lists.
- merge(start, mid, end);
- This function will take two linked lists as input. Then it will recursively merge the two sorted linked lists.
Algorithm to Sort Linked Lists
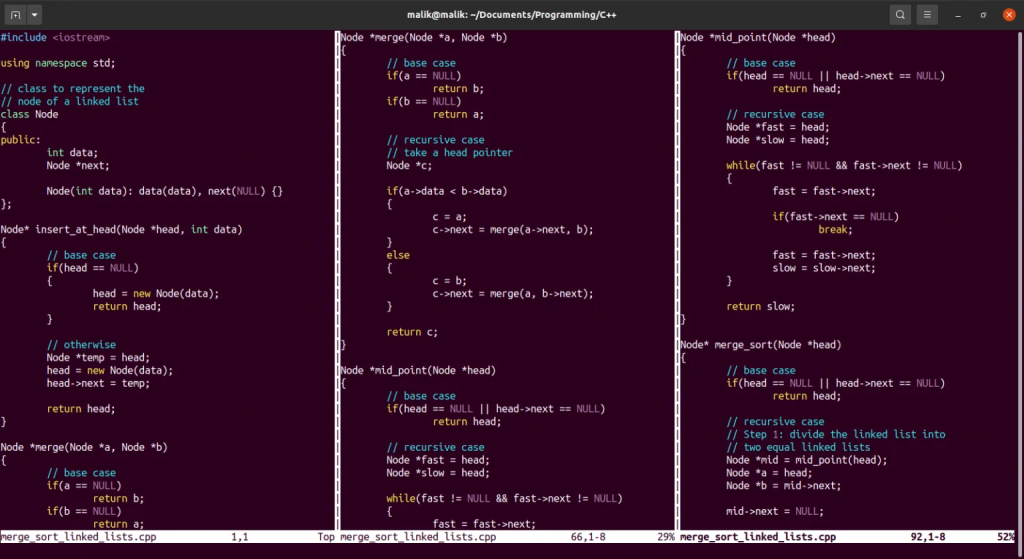
Node *merge(Node *a, Node *b)
{
// base case
if(a == NULL)
return b;
if(b == NULL)
return a;
// recursive case
// take a head pointer
Node *c;
if(a->data < b->data)
{
c = a;
c->next = merge(a->next, b);
}
else
{
c = b;
c->next = merge(a, b->next);
}
return c;
}
Node *mid_point(Node *head)
{
// base case
if(head == NULL || head->next == NULL)
return head;
// recursive case
Node *fast = head;
Node *slow = head;
while(fast != NULL && fast->next != NULL)
{
fast = fast->next;
if(fast->next == NULL)
break;
fast = fast->next;
slow = slow->next;
}
return slow;
}
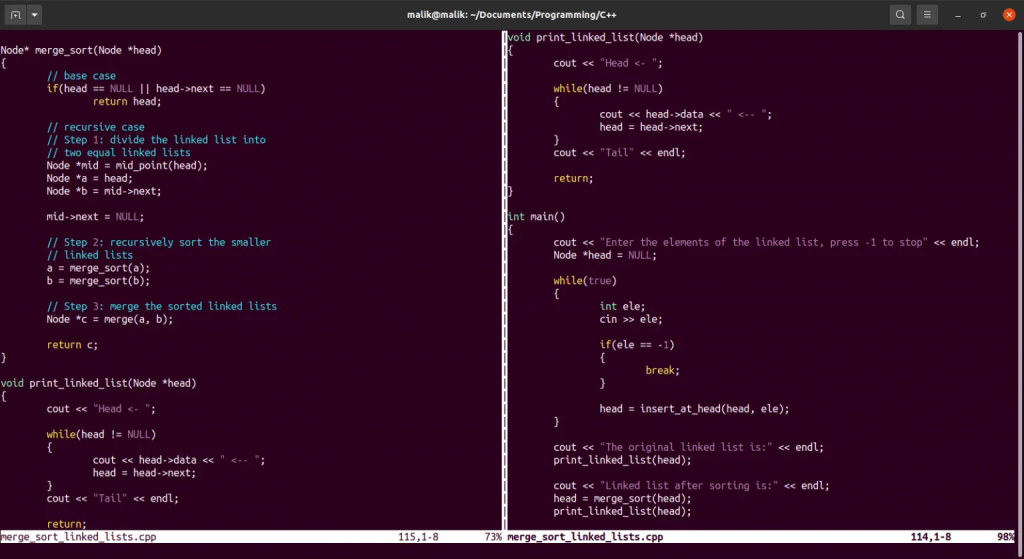
Node* merge_sort(Node *head)
{
// base case
if(head == NULL || head->next == NULL)
return head;
// recursive case
// Step 1: divide the linked list into
// two equal linked lists
Node *mid = mid_point(head);
Node *a = head;
Node *b = mid->next;
mid->next = NULL;
// Step 2: recursively sort the smaller
// linked lists
a = merge_sort(a);
b = merge_sort(b);
// Step 3: merge the sorted linked lists
Node *c = merge(a, b);
return c;
}
Sort Linked Lists Using C++ Program
Let’s now write a program to sort linked lists using C++.
#include <iostream>
using namespace std;
// class to represent the
// node of a linked list
class Node
{
public:
int data;
Node *next;
Node(int data): data(data), next(NULL) {}
};
Node* insert_at_head(Node *head, int data)
{
// base case
if(head == NULL)
{
head = new Node(data);
return head;
}
// otherwise
Node *temp = head;
head = new Node(data);
head->next = temp;
return head;
}
Node *merge(Node *a, Node *b)
{
// base case
if(a == NULL)
return b;
if(b == NULL)
return a;
// recursive case
// take a head pointer
Node *c;
if(a->data < b->data)
{
c = a;
c->next = merge(a->next, b);
}
else
{
c = b;
c->next = merge(a, b->next);
}
return c;
}
Node *mid_point(Node *head)
{
// base case
if(head == NULL || head->next == NULL)
return head;
// recursive case
Node *fast = head;
Node *slow = head;
while(fast != NULL && fast->next != NULL)
{
fast = fast->next;
if(fast->next == NULL)
break;
fast = fast->next;
slow = slow->next;
}
return slow;
}
Node* merge_sort(Node *head)
{
// base case
if(head == NULL || head->next == NULL)
return head;
// recursive case
// Step 1: divide the linked list into
// two equal linked lists
Node *mid = mid_point(head);
Node *a = head;
Node *b = mid->next;
mid->next = NULL;
// Step 2: recursively sort the smaller
// linked lists
a = merge_sort(a);
b = merge_sort(b);
// Step 3: merge the sorted linked lists
Node *c = merge(a, b);
return c;
}
void print_linked_list(Node *head)
{
cout << "Head <- ";
while(head != NULL)
{
cout << head->data << " <-- ";
head = head->next;
}
cout << "Tail" << endl;
return;
}
int main()
{
cout << "Enter the elements of the linked list, press -1 to stop" << endl;
Node *head = NULL;
while(true)
{
int ele;
cin >> ele;
if(ele == -1)
{
break;
}
head = insert_at_head(head, ele);
}
cout << "The original linked list is:" << endl;
print_linked_list(head);
cout << "Linked list after sorting is:" << endl;
head = merge_sort(head);
print_linked_list(head);
return 0;
}
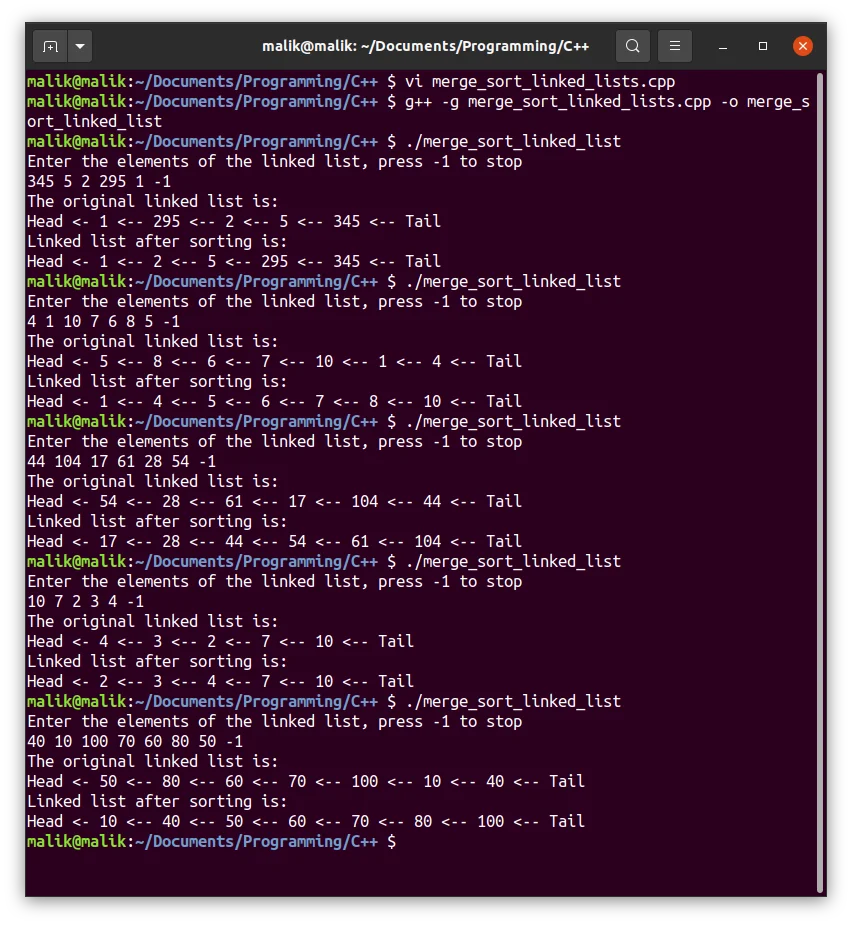
Output
Conclusion
In this article, we learned to sort a linked list using the merge sort algorithm. This is one of the most optimized methods to sort a linked list and can work for lists of the size 106. That’s all for today, thanks for reading.
Further Readings
To learn more about sorting and linked lists, you can go through the following articles.
https://www.temp.vm-help.com/56329/merge-sort-in-cpp
https://www.temp.vm-help.com/55647/linked-lists-cpp





