Robot And Paths Problem Using Dynamic Programming in C++

Today, we’ll learn to solve robot and paths problem using dynamic programming in C++. It’s a popular dynamic programming problem on CodeChef. Dynamic programming is a great way to solve problems that revolve around paths. So without wasting time, let’s get started.

Problem Statement for Robot And Paths Problem

Given a grid of size (M x N). A robot enters the grid from the coordinates (0, 0). Some cells of the grid are blocked. Find out the total number of ways the robot can take to reach the cell (M – 1, N – 1). Note: the motion of the robot is limited to one step towards the South or one step towards the east.

Input Format

The first line of the input will be the dimensions of the grid i.e. R, C and the number of cells blocked in the grid. The following P lines will contain the coordinates of the blocks.

For example,

Input:
4 3 2
3 3
3 1

Solution:
2

Approach

How To Deal With Dynamic Programming Problems

In dynamic programming, we never waste our previous computations. This distinguishes dynamic programming from recursion. We use dynamic programming because it makes the solution many times more optimum than recursive solutions.

Pseudocode

Below is the step-by-step process that we’ll follow to code the solution.

To reach the cell (i, j), we can only come through two paths.
- Through (i – 1, j)
  - By descending one level from the upper row.
- Or through (i, j – 1)
  - By moving one step towards the east.
Create a 2D array to store the answers to smaller subproblems.
The total number of ways for each cell is the result of the recursive relation.
- Recusive relation: dp[i][j] = dp[i – 1][j] + dp[i][j – 1];
We’ll check for the base cases first.
- if(i == 0 || j == 0)
- It represents either the topmost row or the leftmost column.
- There’s only a single way to reach the elements in these rows, given that there’s no block.
If top cell is blocked : dp[i][j] = dp[i][j – 1]
If left cell is blocked : dp[i][j] = dp[i – 1][j]
We’ll do this for all the cells. And store the answers in a dynamic programming array.

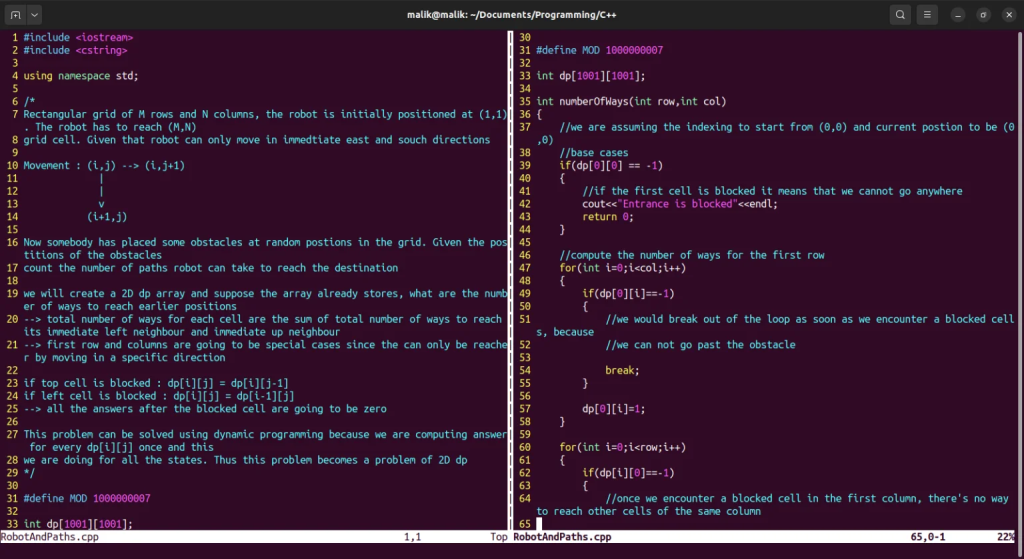
Robot And Paths Problem Using Dynamic Programming In C++ Program

#include <iostream>
#include <cstring>

using namespace std;

#define MOD 1000000007

int dp[1001][1001];

int numberOfWays(int row,int col)
{
	//we are assuming the indexing to start from (0,0) and current postion to be (0,0)
	//base cases
	if(dp[0][0] == -1)
	{
		//if the first cell is blocked it means that we cannot go anywhere 
		cout<<"Entrance is blocked"<<endl;
		return 0;
	}

	//compute the number of ways for the first row
	for(int i=0;i<col;i++)
	{
		if(dp[0][i]==-1)
		{
			//we would break out of the loop as soon as we encounter a blocked cells, because 
			//we can not go past the obstacle

			break;
		}

		dp[0][i]=1;
	}

	for(int i=0;i<row;i++)
	{
		if(dp[i][0]==-1)
		{
			//once we encounter a blocked cell in the first column, there's no way to reach other cells of the same column

			break ;
		}

		dp[i][0]=1;
	}

	//now that we have finished marking the first row and first column, we will create the rest of the grid

	for(int i=1;i<row;i++)
	{
		for(int j=1;j<col;j++)
		{
			cout<<"i:j is : ";
			cout<<i<<" "<<j<<endl;
			if(dp[i][j]==-1)
			{
				cout<<"dp["<<i<<"]["<<j<<"] is blocked : "<<dp[i][j]<<endl;
				continue;
			}

			dp[i][j]=0;

			//check if the cell on the left is blocked or not
			//if the cell is found blocked then we will skip its value in the sum

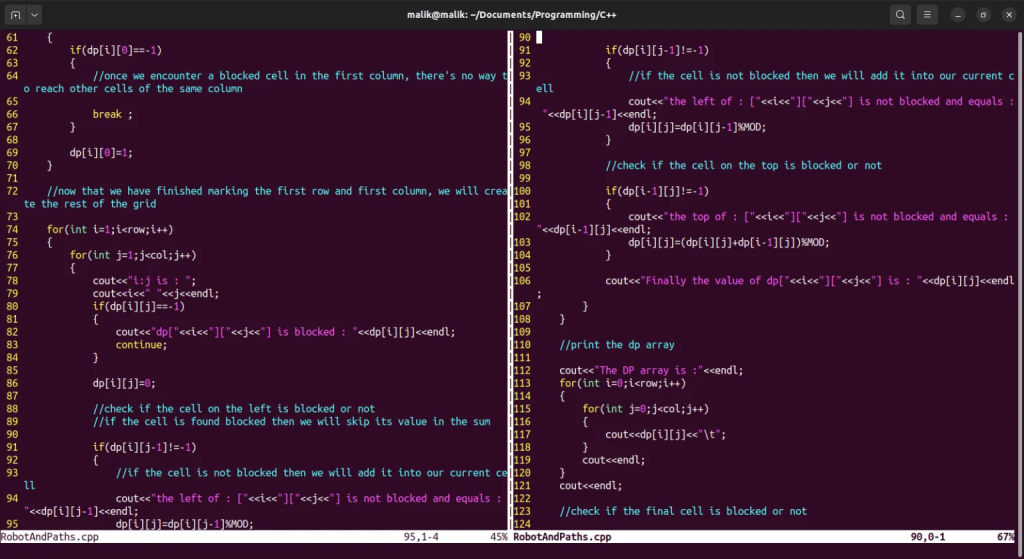
			if(dp[i][j-1]!=-1)
			{
				//if the cell is not blocked then we will add it into our current cell
				cout<<"the left of : ["<<i<<"]["<<j<<"] is not blocked and equals : "<<dp[i][j-1]<<endl;
				dp[i][j]=dp[i][j-1]%MOD;
			}

			//check if the cell on the top is blocked or not 

			if(dp[i-1][j]!=-1)
			{
				cout<<"the top of : ["<<i<<"]["<<j<<"] is not blocked and equals : "<<dp[i-1][j]<<endl;
				dp[i][j]=(dp[i][j]+dp[i-1][j])%MOD;
			}

			cout<<"Finally the value of dp["<<i<<"]["<<j<<"] is : "<<dp[i][j]<<endl;
		}
	}

	//print the dp array 

	cout<<"The DP array is :"<<endl;
	for(int i=0;i<row;i++)
	{
		for(int j=0;j<col;j++)
		{
			cout<<dp[i][j]<<"\t";
		}
		cout<<endl;
	}
	cout<<endl;

	//check if the final cell is blocked or not 

	if(dp[row-1][col-1]==-1)
	{
		return 0;
	}

	cout << "Ans: ";
	return dp[row-1][col-1];
}

int main()
{
	memset(dp,0,sizeof dp);

	cout << "Enter tihe values of M, N, and P" << endl;
	int M,N,P; //M is number of row,N number of columns
	cin>>M>>N>>P;

	cout << "Enter the locations of blocks" << endl;
	for(int i=0;i<P;i++)
	{
		int x,y;
		cin>>x>>y;

		//mark all the blocked cells 

		dp[x-1][y-1]=-1;	
	}

	cout<<"Initially the DP array is :"<<endl;
	for(int i=0;i<M;i++)
	{
		for(int j=0;j<N;j++)
		{
			cout<<dp[i][j]<<"\t";
		}
		cout<<endl;
	}
	cout<<endl;

	cout<<numberOfWays(M,N)<<endl;

	return 0;
}

Output

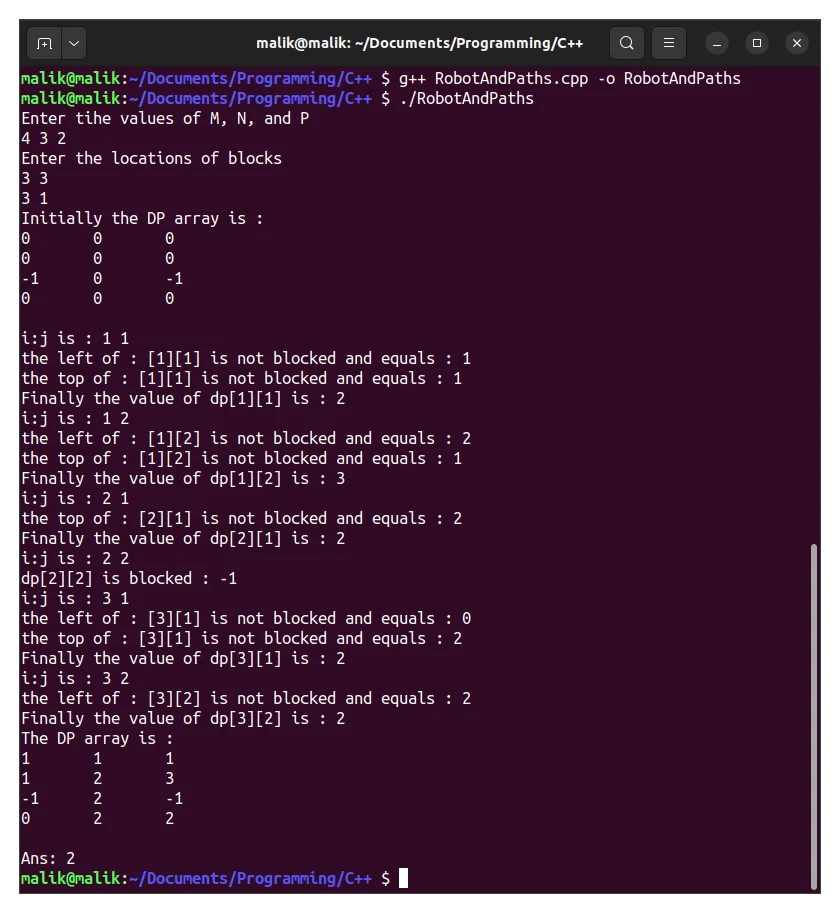
Conclusion

Today, we solved the robots and paths problem dynamic programming in C++. We used the concept of recursion + memoisation(Dynamic Programming) to solve this problem. We used the bottom-up approach to develop this solution. In the end, we implemented a C++ program to demonstrate the working of our solution. That’s all for today, thanks for reading.