Today, we’ll learn to solve the optimal game strategy problem using C++ and dynamic programming. It’s a popular dynamic programming problem on LeetCode. Dynamic programming is one of the toughest concepts of data structures and algorithms. So without wasting time, let’s get started.
Also read: Friends Pairing Problem Using Dynamic Programming In C++
Problem Statement
You are playing a game against your computer. There are 2 * N coins placed in an array, and each of these entries has a certain fixed value. There will be N chances for each play. During each turn, the active player would select a coin from either of the ends. The sum of the coins collected by each player at the end decides the winner. Assume that you and the computer are equally smart at playing this game. Find the maximum score that you can obtain against the computer if you start first.
Input Format
The input will be a single integer N. And the following line will contain N integers representing the value of coins.
For example,
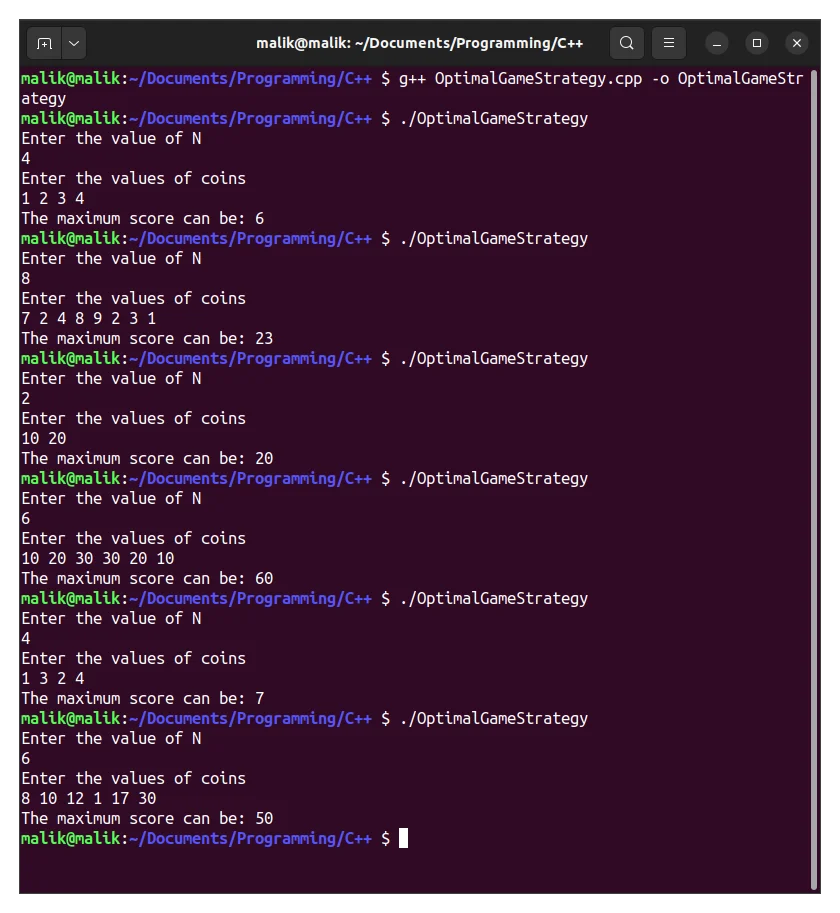
n: 4
array: 1 2 3 4
Ans: 6 = 4 + 2
Approach for Optimal Game Strategy
The recursive approach is not enough for large values of N. The time complexity of the recursive solution is exponential with the number of turns(i.e. time complexity = O(2N)). The recursive solution is functional only up to N = 24.
Also read: Greedy Problem Expedition Using C++
How To Deal With Dynamic Programming Problems
Dynamic programming problems are recursive problems but by storing the intermediate states, we reduce a large number of recomputations. Similar to recursive solutions, dynamic programming solutions compute all the subproblems of a problem but we store our solutions using some data structure.
Dynamic Programming = Recursion + Memoisation = Never solve the same problem twice
Recursion: Compute all the subproblems of a problem.
Memoization: Store the results of expensive computations.
Pseudocode
Below is the step-by-step process that we’ll follow to code the solution.
- Each player can pick a number from each end.
- Both the players are equally wise.
- Choose the maximum profit for yourself and leave behind the minimum profit choices for the computer
- f(i,j)= max(a[i] + min(f(i+1, j-1), f(i+2, j)), a[j] + min(f(i, j-2), f(i-1, j-1)))
- Score if you select the leftmost element:
- a[i] + min(f(i+1,j-1), f(i+2, j));
- If you select the rightmost element:
- a[j] + min(f(i, j-2), f(i-1, j-1))
Recurrence Relation
f(i,j)= max(a[i] + min(f(i+1, j-1),f(i+2, j)), a[j] + min(f(i, j-2),f(i-1, j-1)))
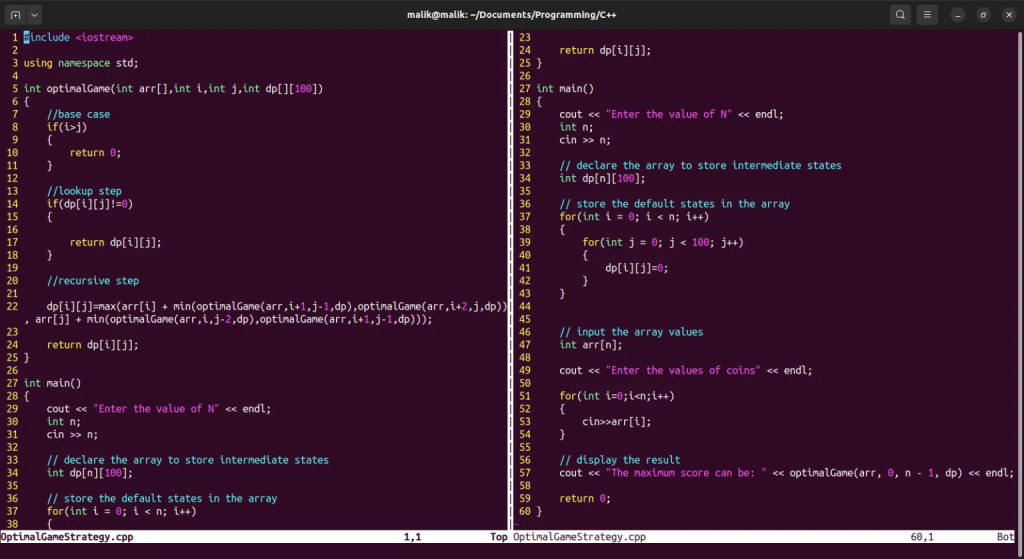
Optimal Game Strategy Problem Using C++ Program
#include <iostream>
using namespace std;
int optimalGame(int arr[],int i,int j,int dp[][100])
{
//base case
if(i>j)
{
return 0;
}
//lookup step
if(dp[i][j]!=0)
{
return dp[i][j];
}
//recursive step
dp[i][j]=max(arr[i] + min(optimalGame(arr,i+1,j-1,dp),optimalGame(arr,i+2,j,dp)), arr[j] + min(optimalGame(arr,i,j-2,dp),optimalGame(arr,i+1,j-1,dp)));
return dp[i][j];
}
int main()
{
cout << "Enter the value of N" << endl;
int n;
cin >> n;
// declare the array to store intermediate states
int dp[n][100];
// store the default states in the array
for(int i = 0; i < n; i++)
{
for(int j = 0; j < 100; j++)
{
dp[i][j]=0;
}
}
// input the array values
int arr[n];
cout << "Enter the values of coins" << endl;
for(int i=0;i<n;i++)
{
cin>>arr[i];
}
// display the result
cout << "The maximum score can be: " << optimalGame(arr, 0, n - 1, dp) << endl;
return 0;
}
Output
Conclusion
Today, we solved the optimal game strategy problem using C++ and dynamic programming. We used the concept of recursion + memoisation(Dynamic Programming) to solve this problem. Dynamic programming solutions are of two types. The first is the bottom-up approach and the second one is the top-down approach. In this article, we used the top-down approach to develop this solution In the end, we implemented a C++ program to demonstrate the working of our solution. The time and the space complexity of this approach is O(N). That’s all for today, thanks for reading.





