NumPy.average() in Python: Calculating Average of NumPy Arrays

NumPy is a quite handy tool in Python for math stuff. Ever heard of numpy.average()? It’s like a quick math helper, making average calculations a breeze! Let’s explore the core concept of averages and understand the numpy.average() function with the definitions of its parameters in detail and also some real-life examples to promote higher clarity in the concepts. So let’s begin.

An Overview of Average

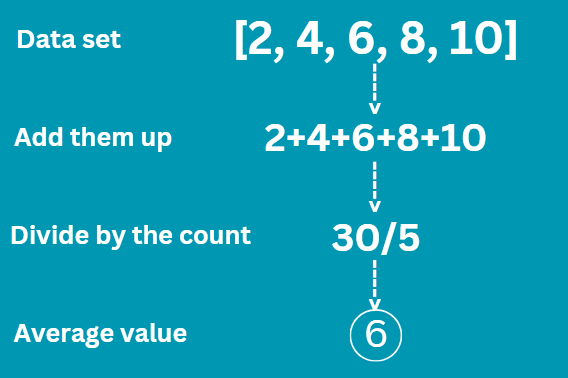
An average is a way to figure out what most of the numbers in a group are like. It’s similar to finding a ‘middle’ value.

Suppose you have a bunch of numbers, like 2, 4, 6, 8, and 10. Now, if you want to know a single number that represents these numbers as a whole, you can find their average. To achieve it you start by adding all these numbers together. So, 2 + 4 + 6 + 8 + 10 = 30. Then, you divide this sum by how many numbers you added together. Since there are 5 numbers, you divide 30 by 5. After doing the division, you get 6. So, 6 is the average of these numbers.

Introduction to NumPy.average()

The numpy.average() is a function in the NumPy library of Python that helps you find different types of averages from a set of numbers.

The syntax of this method looks something like this:

numpy.average(a, axis=None, weights=None, returned=False)

Let’s try to understand what these parameters mean.

a: This is the bunch of numbers you want to find the average of.
axis: This part is optional. It lets the function know if you want to find the average along a particular direction in a multi-dimensional array.
weights: This parameter allows you to give different importance or ‘weights’ to each value in the array. If you provide weights, the function will use them to calculate a weighted average instead of a regular one.
returned: This part is for deciding if you want extra information from the function. When returned=True, the function also gives back the sum of the weights (if weights are given), along with the average.

Examples of NumPy.average()

I see, you might be confused by the above parameters. Let’s understand their use with some real examples.

Example 1

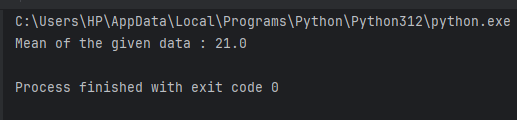
Let’s start with calculating the basic mean using the numpy.average(). Here we will calculate the average of the numbers in the data and print it.

import numpy as np

data = np.array([7, 14, 21, 28, 35])
mean = np.average(data)
print("Mean of the given data :", mean)

Output:

Example 2

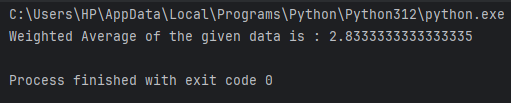
In this example, we will calculate the weighted mean of the given data. Look at the code below:

import numpy as np

data = np.array([3, 2])
weights = np.array([1, 0.2])
weighted_avg = np.average(data, weights=weights)
print("Weighted Average of the given data is :", weighted_avg)

In this case, the first number (3) has a weight of 1, while the second number (2) has a weight of 0.2.To find the weighted average, we multiply each number by its weight. Then, we sum up these products: 3 + 0.4 = 3.4. Finally, we divide the sum of the products by the total weight:

Example 2 Illustration — Calculation of weighted mean

So, the weighted average of the numbers 3 and 2, with weights 1 and 0.2 respectively, is approximately 2.8333.

Output:

Example 3

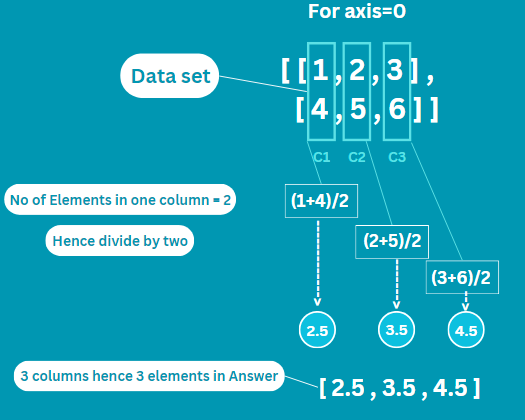
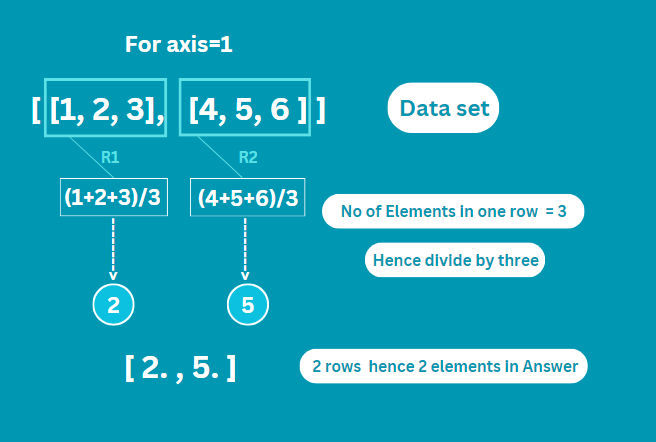
Let’s try to use the axis parameter in this example, Axis 0 stands for columns , and axis 1 stands for rows. So, when we say axis=0, we’re finding averages column by column, and with axis=1, we’re finding averages row by row. Here’s the code:

import numpy as np

data = np.array([[1, 2, 3],
                 [4, 5, 6]])
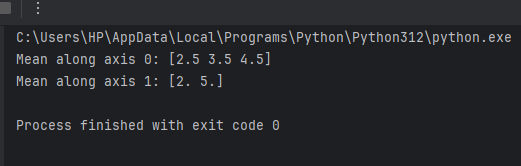
mean_axis_0 = np.average(data, axis=0)
print("Mean along axis 0:", mean_axis_0)
mean_axis_1 = np.average(data, axis=1)
print("Mean along axis 1:", mean_axis_1)

Example 3 Illustration — Column wise average

Example 3 Illustration 2 — Row wise average

Output:

Summary

And yes, it’s the bottom line! I hope that after reading this article, you have gained knowledge about the concept of average and the method of calculating average with ease in Python using numpy.average. We have also covered the three most important parameters and have calculated all types of averages including simple mean, weighted mean, mean around axis, etc. Now it’s time for you to experiment with the function.

Further Reading: