Minimum Cost Path Using Dynamic Programming in C++

Today, we’ll learn to solve the problem of finding the minimum cost path using dynamic programming in C++. It’s a popular dynamic programming problem on LeetCode, CodeForces, and CodeChef. Dynamic programming is a great choice to solve the minimum cost path and maximum cost path problems. So without wasting time, let’s get started.

Problem Statement for Minimum Cost Path

You are standing in a maze of size M x N units. Some cells of the maze might be blocked. You are standing at the cell (1, 1) in the maze. The cost of traveling through a cell in the maze is the value stored in that cell. Your objective is to reach the cell (x, y) in the maze minimizing the total cost of traversal. Note: You can only travel along the right and the down directions.

Input Format

The input will be a single integer N. And the following line will contain N integers representing the value of coins.

For example,

M: 3 
N: 3

Maze:
1 5 2
7 1 1
8 1 3

X: 2
Y: 2

Solution:
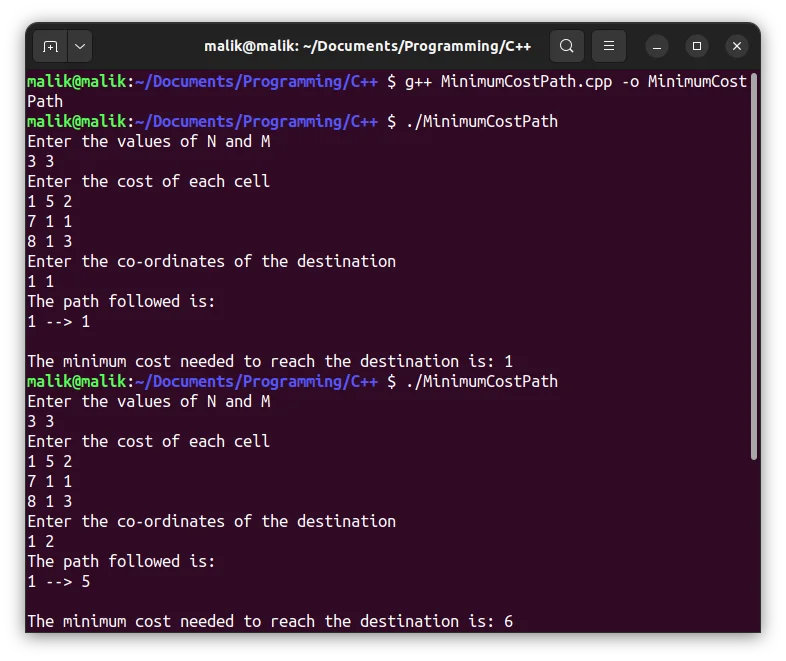
Minimum cost of travel: 7

Path: 1 --> 5 --> 1

Approach for Minimum Cost Path

The recursive approach is not enough for large values of N. The time complexity of the recursive solution is exponential with the number of turns(i.e. time complexity = O(2^N)). The recursive solution is functional only up to N = 24.

How To Deal With Dynamic Programming Problems

Dynamic programming problems are recursive problems but by storing the intermediate states, we reduce a large number of recomputations. Similar to recursive solutions, the dynamic programming solutions compute all the subproblems of a problem but we store our solutions using some data structure.

Dynamic Programming = Recursion + Memoisation = Never solve the same problem twice

Recursion: Compute all the subproblems of a problem.

Memoisation: Store the results of expensive computations.

Pseudocode

Below is the step by step process that we’ll follow to code the solution.

• Base cases:
  1. (i == 0 && j == 0): dp[i][j] = cost[0][0];
  2. i == 0: dp[i][j] = dp[0][j – 1] + cost[i][j];
  3. j == 0: dp[i][j] = dp[i][0] + cost[i][j];
• Recursive case:
  • We can reach the cell (i, j) using two routes
    1. Through (i – 1, j)
    2. Or via, (i, j – 1)
  • Our answer will be the minimum of both the paths.
  • dp[i][j]=min(dp[i – 1][j], dp[i][j – 1]) + cost[i][j];
• Store this value in the dp[i][j] cell of the dynamic programming array. And use this variable later to avoid the computation of pre-computed subproblems.

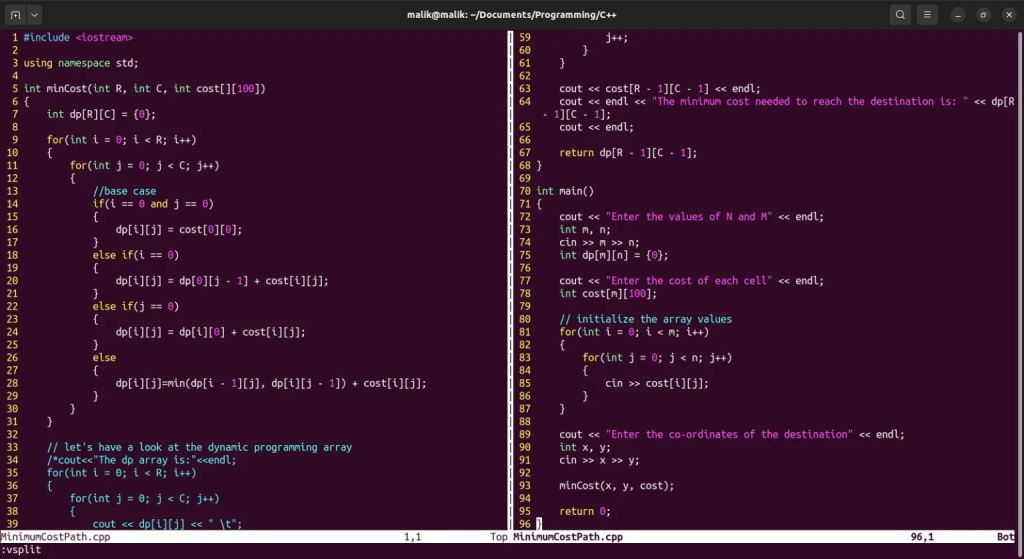
Minimum Cost Path Using Dynamic Programming In C++ Program

#include <iostream>

using namespace std;

int minCost(int R, int C, int cost[][100])
{
	int dp[R][C] = {0};

	for(int i = 0; i < R; i++)
	{
		for(int j = 0; j < C; j++)
		{
			//base case 
			if(i == 0 and j == 0)
			{
				dp[i][j] = cost[0][0];
			}
			else if(i == 0)
			{
				dp[i][j] = dp[0][j - 1] + cost[i][j];
			}
			else if(j == 0)
			{
				dp[i][j] = dp[i][0] + cost[i][j];
			}
			else 
			{
				dp[i][j]=min(dp[i - 1][j], dp[i][j - 1]) + cost[i][j];
			}
		}
	}

	// let's have a look at the dynamic programming array
	/*cout<<"The dp array is:"<<endl;
	for(int i = 0; i < R; i++)
	{
		for(int j = 0; j < C; j++)
		{
			cout << dp[i][j] << " \t";
		}

		cout << endl;
	}*/

	//tracing our path 
	cout << "The path followed is: " << endl;
	cout << cost[0][0] << " --> ";
	int i = 0,j = 0;
	while(i < R - 1 && j < C - 1)
	{
		if(dp[i + 1][j] < dp[i][j + 1])
		{
			cout << cost[i + 1][j]<< " --> ";
			i++;
		}
		else
		{
			cout << cost[i][j + 1] << " --> ";
			j++;
		}
	}

	cout << cost[R - 1][C - 1] << endl;
	cout << endl << "The minimum cost needed to reach the destination is: " << dp[R - 1][C - 1];
	cout << endl;

	return dp[R - 1][C - 1];
}

int main()
{
	cout << "Enter the values of N and M" << endl;
	int m, n;
	cin >> m >> n;
	int dp[m][n] = {0};

	cout << "Enter the cost of each cell" << endl;
	int cost[m][100];

	// initialize the array values
	for(int i = 0; i < m; i++)
	{
		for(int j = 0; j < n; j++)
		{
			cin >> cost[i][j];
		}
	}

	cout << "Enter the co-ordinates of the destination" << endl;
	int x, y;
	cin >> x >> y;
	
	minCost(x, y, cost);

	return 0;
}

Output

Conclusion

Today, we solved the problem of a minimum-cost path using dynamic programming in C++. We used the concept of recursion + memoisation(Dynamic Programming) to solve this problem. Dynamic programming solutions are of two types. The first is the bottom-up approach and the second one is the top-down approach. In this article, we used the bottom-up approach to develop this solution In the end, we implemented a C++ program to demonstrate the working of our solution. The time and the space complexity of this approach is O(N²). That’s all for today, thanks for reading.

Further Readings

To learn more about C++ programming, data structures, and algorithms, you can go through the following articles.

https://www.journaldev.com/56663/breadth-first-search-algorithm-graphs-cpp

https://www.journaldev.com/56532/queue-class-in-cpp