Mathematics has a handful of parameters using which we can gauge numbers. One among those is the square root. It might be a walk to find the square root when the given numbers are the product of themselves, but when it no longer seems to be the case, things get a tad bit difficult.
This article sets out to explore the different ways of using the built-in function – sqrt( ) from the numpy library of Python which is used to calculate the square roots in Python programming. We shall cover the aspects of the sqrt( ) function in the following sections:
- Syntax of sqrt( ) function
- Using sqrt( ) function on One-Dimensional Array
- Using sqrt( ) function on N-Dimensional Array
- Using sqrt( ) function on Complex Numbers
- Limitations of sqrt( ) function
Before that let us import the numpy library using the below code:
import numpy as np
Syntax of sqrt( ) Function
We shall understand the construction of the sqrt( ) function using the syntax given below which details the basic constituents required for its effective functioning.
Syntax:
numpy.sqrt(x, out=None, where=True, dtype=None)
Parameters:
- x – input array or scalar entity for which the square root is to be deduced
- out – an optional construct set to none by default, and can be used to have the results stored in a specific array that is of the same length as the output
- where – an optional construct set to True by default and is used to pass the function at all positions that are declared True and retain those positions as is, which are set to False
- dtype – an optional construct used to specify the data type that is to be returned
Using sqrt( ) Function on One-Dimensional Array
In this section, we shall construct a one-dimensional array using the below code in order to calculate the square root for its elements.
ar1 = [[12, 36, 71, 99]]
Once done, the above array is passed through the sqrt( ) function to find the results.
np.sqrt(ar1)
Output:
Using sqrt( ) Function on N-Dimensional Array
The square root calculation for N-dimensional arrays shall be demonstrated in this section and it works in the same way as done earlier for the one-dimensional array. Given below is a two-dimensional array that shall be passed through the sqrt( ) function to determine the square root of its entities.
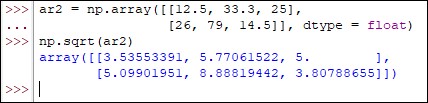
ar2 = np.array([[12.5, 33.3, 25],
[26, 79, 14.5]], dtype = float)
np.sqrt(ar2)
Output:
Using sqrt( ) Function on Complex Numbers
When calculating the square root for decimals with a pen and paper can give you a migraine, imagine what can the square root calculation of complex numbers give you. Just to have a fair idea of what is being implied here, have a look at the below formula to calculate the square root of the complex numbers.
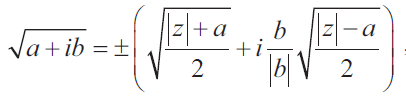
But Python being all the more friendly, has induced the capabilities in the sqrt( ) function for determining the square root of complex numbers too. But it comes with a price! When the input array has a complex number, then the sqrt( ) function goes on to consider every other element in the input as a complex number and deduce its corresponding square root.
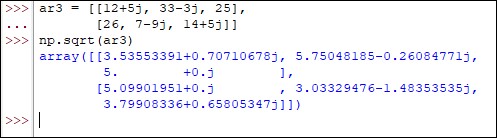
ar3 = [[12+5j, 33-3j, 25],
[26, 7-9j, 14+5j]]
np.sqrt(ar3)
Output:
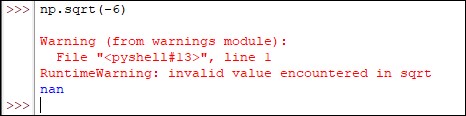
Limitations of sqrt( ) Function
This function is limited to calculating the square roots of only positive numbers. When those that are negative come into the picture, then the below result comes up:
Conclusion
Now that we have reached the end of this article, hope it has elaborated on the different ways to find the square root using the sqrt( ) function from the numpy library. Here’s another article that explains how to use the positive( ) function for N-dimensional arrays in Python. There are numerous other enjoyable & equally informative articles in CodeforGeek that might be of great help to those who are looking to level up in Python. Whilst you enjoy those, adios!
Reference
https://numpy.org/doc/stable/reference/generated/numpy.sqrt.html
