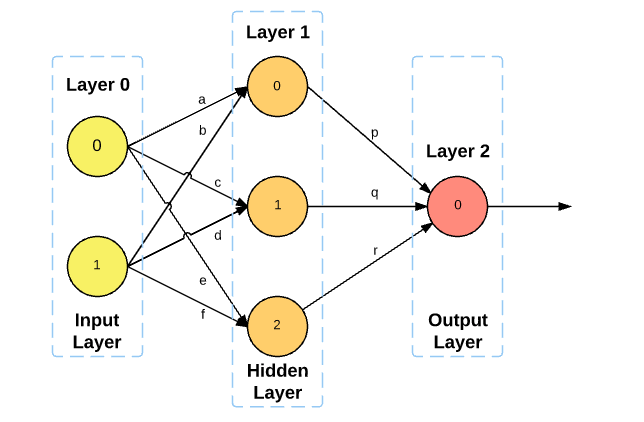
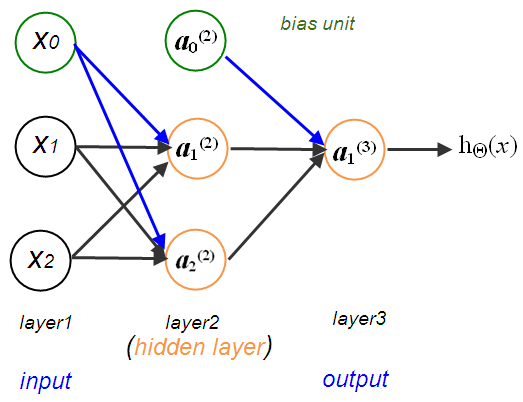
With the rise in the field of machine learning and artificial intelligence, the need for neural networks is also elevating. The neural network comprises a series of algorithms that undertakes to perceive the connection in a data set by a method that is similar to the way the human brain works. They can modify to altering input; as a result, the network engenders better output without reconditioning the output principle.
Building a simple neural network using Python may seem complicated, but with the right approach and steps, it can be done smoothly. Other than the procedure, attention should also be paid to the most common python programming mistakes to get better results.
Steps to build a Simple Neural Network
The structure of the neural network is usually multiplex and involves various layers containing millions of neurons so that they will have the ability to tackle the datasets. Besides, to get a better understanding and command of broad and deep neural networks, to begin with, an easy network is preferable.
Therefore, this article will be about the basic and primary kind of network having dual layers. This task can be accomplished with a limited and accessible dataset.
The function of a neural network depends on multiple variables, as it hauls an input, process computing, and delivers the output. Here are primary steps that are essential to building a simple neural network.
1: Feedforward Propagation
The input X allows the information which reaches the units at all layers to generate the output. The network’s architecture analyzes the width, depth, and activation features for every layer. Depth reflects the count of hidden layers, whereas width shows the count of units on each layer. Also, there are some set activation operations such as Hyperbolic tangent, Sigmoid, and Rectified Liner.
Studies have proven that networks with depth have better efficiency with more hidden units. Hence it is the better approach for a deeper network with lessens rebounds.
2: Visualizing data
The function of a neural network depends on many variables, as it hauls an input, process computing, and delivers the output. To visualize it in the form of neurons in various layers, as every neuron of a single layer is connected to neurons of layers before and after. Entire computing occurs within these neurons and varies on the weights that link the neurons by one another. The critical aspect is to get the correct weights to achieve the intended results.
3: Model Representation
In neural networks, there is a recommendation by analyzing the analytical relapse and putting that in architecture similar to the brain. It has variants as the logistic function is termed as a sigmoid activation feature in addition to the theta parameters as weights.
For the activation unit, the weighted input of every unit in the earlier layer is re-estimated and re-determined. It can be said that neural networks have the effect of executing the idea of a statistical relapse often with higher and advanced input.
4: Cost function
It refers to a measure of the quality of a neural network in regards to the liable sample and intended output. This may also rely on fluctuating biases and weights. Cost function must be considered as a single value and not a vector as it amounts to the attribute of the neural network.
In fact, a cost function is the type of neural network.
Here W is the weight of neural weights, B is a bias of it, S represents the input, and E is the intended output. It is useful to take care of Y i/j and A i/j for any neuron j in layer I, as these two values relay on W, B, and Sr.
5: Sigmoid gradient
The sigmoid function is best suited for the final layer as its ending values range from 0 and 1. Whereas the (hyperbolic tangent) suits more for the hidden layer, however, all other functions used are applicable. The parameters used are the weights W1, W2 and the biases b1, b2. W1 and b1 are the links of the input layer along with the hidden layer, whereas W2 and b2 link the hidden layer with the ending layer. As per the primary rule of Neural Network the activations A1 and A2 are estimated as below:
A2=g(W2*A1+b2)
Here g and h represent the activation functions and W1, W2, b1, b2 are usual patterns. This leads the process to original code by implementing sigmoid activation function as below:
Here z represents a matrix. Besides, NumPy backs calculations with matrices that make coding comparatively easy.
6: Random initialization
In the later part of the process, it requires the implementation of forwarding propagation. The function forward_prop (X, parameters) uses as input for the neural network using matrix X and the parameters vocabulary and rebound the output of the Neural Network A2 along a cache vocabulary to be later used in backpropagation.
This leads to the most challenging step of the Neural Network algorithm that is Backpropagation. The function will rebound the gradients of the loss function in regards to 4 parameters of the network, i.e. (W1, W2, b1, b2).
7: Gradient checking
After getting all the gradients of the loss function, the use of a gradient descent algorithm is done to update the parameters. The implementation of all the tasks required for one circle is done. Now, these will be put within a function from the main program. This function uses as input for matrices X and Y, the units n_x, n_h, n_y, the sum of iterations for the Gradient Descent algorithm to proceed and unite all the functions to return the parameters.
8: Learning parameters
At this step, the function will rebound the parameters of the neural network. The function predicts (X parameters) takes as input for the matrix X for the elements. For this, the computer of the XOR function is needed, and the parameters of the model to rebound the desired result y by using a verge of 0.5.
All the required functions are almost done. Now going to the main program and maintaining the matrices X and Y are done along with the hyperparameters n_x, n_h, n_y, num_of_iters, learning_rate. With this setup, it will be much easier to train the model.
Summary
For learning more about this topic, free python programming courses for beginners can be useful. Besides, to build a more extensive network with multiple layers and hidden units, there will be a need for other variations of the algorithms. The steps above are helpful and may be followed at any level to build a Neural Network using Python.